Exponentialfunktion: Berechnung von Nullstellen, Extrempunkten und Wendepunkten

Question

 Übung zur Berechnung von

- Nullstellen
- Extrempunkten
- Wendepunkten

1) \( f(x)=(x-1) \cdot e^{x} \)
2) \( f(x)=\left(\frac{1}{2} x+\frac{1}{2}\right) \cdot e^{-2 x} \)
3) \( f(x)=(x-2) \cdot e^{0,5 x} \)
4) \( f(x)=(4 x+4) \cdot e^{-0,5 x} \)
5) \( f(x)=x \cdot e^{2-x} \)
6) \( f(x)=\left(x^{2}-x\right) \cdot e^{0,5 x} \)

Comments

Nullstelcen
- Extrempunteter
- Wendepiunteten

Also echt jetzt.

Answer 1

Funktion und Ableitungen

f(x) = e^x·(x - 1)
f'(x) = e^x·x
f''(x) = e^x·(x + 1)

Nullstellen

f(x) = e^x·(x - 1) = 0 → x = 1

Extrempunkte

f'(x) = e^x·x = 0 → x = 0
f(0) = e^0·(0 - 1) = -1 → TP(0 | -1)

Wendepunkte

f''(x) = e^x·(x + 1) = 0 → x = -1
f(-1) = e^{-1}·(-1 - 1) = -2/e ≈ -0.7358 → WP(-1 | -2/e)

Comments

abakus, kannst du mir 1 eins wenigstens machen, damit ich es verstehe

Wenn du Probleme hast, etwas zu verstehen, frag gerne nach. Ansonsten empfehle ich, dass du es selber mal probierst.

Zum Vergleich deiner Lösungen kannst du einen Onlinerechner wie https://funktion.onlinemathe.de benutzen.

---

so sieht meine ableitung aus

Text erkannt:

\( \begin{array}{l}f(x)=\underbrace{(x-1)}_{u} \cdot e^{e^{x}} \\ f(x)=e^{x}+e^{x} \cdot(x-1) e^{x}\end{array} \)

---

Achte auf richtige Verwendung der Klammern. Und vereinfache.

---

ist es sonst richtig

---

Sonst, wenn Du das nicht machst, ist es nicht richtig. Denn zweimal Klammer auf und einmal Klammer zu ist immer falsch. Und wenn Du das machst was Nudger geschrieben hat, dann wirst Du dasselbe Ergebnis haben wie der Mathecoach in der 2. Gleichung seiner Antwort.

Answer 2

Hallo

Da e-funktionen immer ungleich 0 sind, musst du nur jeweiligen Klammern oder Vorfaktoren 0 setzen und das kannst du sicher.

gruß lul

Answer 3

Sei gegrüßt!

Hier eine Liste, wie du vorgehen kannst:

• Nullstellen

Die Funktion exp ∘ h (h ist eine Funktion) hat keine Nullstellen. Daher musst du gucken, wann der andere Faktor verschwindet.

• Extrempunkte

Das sind die Nullstellen des Differentials der jeweiligen Funktion, welche bei dem Differenzial zweiten Grades keine Nullstellen sind.

• Wendepunkte

Das sind die Extrempunkte des Differentials.

Liebe Grüße

Detli Black

Comments

Das sind die Nullstellen des Differentials der jeweiligen Funktion, welche bei dem Differenzial zweiten Grades keine Nullstellen sind.

Und da willst Mathematiker sein???

Hochschwülstiges Gelaber, das durch ein einziges Gegenbeispiel blamabel entzaubert wird...

Dann noch diese subtile Fremdenfeindlichkeit:

Ich glaube der Fragesteller ist nicht deutsch sondern ein Flüchtling :)

Es ist mit viel größerer Wahrscheinlichkeit ein Bio-Deutscher, der seinen verschwommenen Aufgabentext mit einer "Texterkennung" abgescannt hat und zu faul war, die sich daraus ergebenden Übersetzungsfehler manuell zu korrigieren.

---

abakus, kannst du mir 1 eins wenigstens machen, damit ich es verstehe

---

Stand nicht mal der Verdacht im Raum, dass es sich um Txman handelt? Was soll denn schon wieder die unnötige Verwendung von Begriffen, die eher keine Hilfe darstellt?

---

Liebe Freunde,

dann soll der Fragesteller einen vernünftigen Sprachgebrauch verwenden um hier zu kommunizieren. Wenn man seinen Text liest (den hat er jetzt geändert), dann klingt das in der Tat nach dem, was ich behauptet habe.

Außerdem verstehe ich nicht, was mit Verdacht Txman gemeint sein soll?

Liebe Grüße

Detli Black

---

dann soll der Fragesteller einen vernünftigen Sprachgebrauch verwenden um hier zu kommunizieren. Wenn man seinen Text liest (den hat er jetzt geändert), dann klingt das in der Tat nach dem, was ich behauptet habe.

Ich habe die Fragestellung korrigiert. Vorher stand dort sicher ein automatisch erkannter Text von der Texterkennung dieser Seite. Wenn die Schreiber ihre Aufgabe sehr unleserlich aufschreiben, dann hat die Texterkennung Probleme.

Aus dem Zusammenhang konnte man aber denke ich erkennen, was gemeint ist. Daher habe ich das korrigiert.

---

dann soll der Fragesteller einen vernünftigen Sprachgebrauch verwenden um hier zu kommunizieren. Wenn man seinen Text liest (den hat er jetzt geändert), dann klingt das in der Tat nach dem, was ich behauptet habe.

Schade, dass du die Kritik nicht verstanden hast und nun dem Fragesteller den schwarzen Peter zuspielst. Es ging darum, dass DU einen übertriebenen mathematischen Sprachgebrauch verwendest, indem du Notationen wie \(\mathrm{exp}\circ h\) oder Begriffe wie Differential verwendest, womit der Fragesteller mit hoher Wahrscheinlichkeit nichts anfangen kann. Das Problem ist also nicht die Fragestellung (denn es war eindeutig erkennbar, worum es geht), sondern dein - ich zitierte - "hochschwülstiges Gelaber", was keine adäquate Hilfe darstellt.

---

Hallo Apfelmännchen @Apfelmännchen,

ich kann es leider nicht nachvollziehen, warum diese Begriffe nach deiner Sicht so schwer zu verstehen sein sollen.

Der Begriff des Differenzials wird oft als  Synonym für eine Ableitungsfunktion verwendet. Sogar wenn das mathematisch nicht ganz korrekt ist, wird es trotzdem gerne gemacht. Außerdem leben wir im digitalen Zeitalter. Das heißt, der Fragesteller kann den Begriff recherchieren, außer er ist unter den Homo neanderthalensis gruppiert.

Die Komposition zweier Abbildungen sollte einem Schüler auch klar sein. Sie kennen das noch unter dem Begriff einer Verkettungsfunktion.

Liebe Grüße

Detlef Schwarzenreiter

---

Wenn die Leute alles im Internet nachschlagen würden, bräuchte es diese Plattform nicht.

was ist denn bitte an diesen Begriffen so schwer zu verstehen?

Und genau diese "herablassende" Art ist hier einfach Fehl am Platz. Man muss die Leute dort abholen, wo sie stehen und nicht wo sie laut ihren Lehrplänen oder was auch immer eigentlich stehen sollten, denn das weicht häufig sehr weit voneinander ab. Zumal diese Plattform sich wohl überwiegend auch an diejenigen richtet oder zumindest von denjenigen genutzt wird, die eben Schwierigkeiten haben. Da darf und kann man einfach nicht erwarten, dass sämtliche Begriffe und Notationen geläufig sind, vor allem, wenn man nicht einmal weiß, ob sie so auch im Unterricht genannt wurden.

Sicherlich könnte man das auch alles recherchieren, allerdings findet man da häufig viel zu viel, was dann nur noch weitere Verwirrung stiftet und damit auch nicht zielführend ist. Wie gesagt, würden die Leute das tun, bräuchte es diese Plattform nicht (viele schaffen es ja nicht einmal, mit ihren eigenen Unterlagen zu arbeiten und sich dort die Beispiele anzuschauen).

Du solltest also einfach nicht vergessen, dass du hier überwiegend mit Menschen arbeitest, die wenig bis keine Ahnung haben bzw. keine Experten des Fachs sind.

---

Bist du nicht Mathematiker?

---

Das hat doch keine Relevanz.

---

Ja eben schon. Als Mathematiker/in sollte man doch am meisten versuchen den schönen mathematischem Sprachgebrauch nicht zu vermeiden.

---

Dann hast du den Kern meines Kommentars nicht verstanden, aber das wundert mich nicht.

---

Du hast den Sinn des Forum nicht verstanden. Es geht nicht darum als Mathematiker zu glänzen, sondern als jemand, der die Situation eines Fragenden versteht und dazu passend Hilfe bietet.

---

Helfen heißt aber auch nicht den Kindern hier alle Arbeit abzunehmen. Sie müssen auch selbst etwas leisten.

---

Das ist im Kern sicherlich nicht falsch, dennoch muss man sich dem Niveau anpassen, wenn man gute Hilfe leisten möchte.

Wenn dir das zu "primitiv" ist, dann ist das hier einfach der falsche Ort für dich.

---

Helfen heißt aber auch nicht den Kindern hier alle Arbeit abzunehmen. Sie müssen auch selbst etwas leisten.

Hau nicht so auf die Kacke und kehre erst mal vor deiner eigenen Haustür!

Deine hochgestochene Behauptung

Das sind die Nullstellen des Differentials der jeweiligen Funktion, welche bei dem Differenzial zweiten Grades keine Nullstellen sind.

- ich übersetze mal -

"Für Extremstellen muss die erste Ableitung 0 sein und die zweite Ableitung darf nicht 0 sein"

ist dummer Bullshit. Jeder einigermaßen veranlagte Schüler kann dir ein Gegenbeispiel nennen.

---

Falls der Antwortgeber noch nicht soweit sein sollte an seiner Schule: Ein Gegenbeispiel ist f(x) = x^4   Das kommt dann im Gymnasium.

---

Du musst doch dem fachlich extrem hilfebedürftigen IMD nicht alles vorsagen.

Er hat doch selbst geschrieben:

Helfen heißt aber auch nicht den Kindern hier alle Arbeit abzunehmen. Sie müssen auch selbst etwas leisten.

---

Lieber abakus,

du hast anscheinend meinen Satz nicht richtig übersetzen können! Bitte lies richtig.

Übersetzt heisst es:

,,Extremstellen sind die Inputs, an der die erste Ableitungsfunktion verschwindet und die zweite Ableitung nicht verschwindet‘‘

Denn würde die zweite Ableitung an diesem Input auch verschwinden, so wäre dies eine Sattelstelle.

Gruß

Detlef Schwarzenreiter

---

Das war jetzt ein peinliches Eigentor, weil du nicht verstanden hast, dass deine Aussage schlichtweg nicht korrekt ist. Diese Inkompetenz untermauerst du mit

Denn würde die zweite Ableitung an diesem Input auch verschwinden, so wäre dies eine Sattelstelle.

Ganz im Stile von Txman. :)

---

Apfelmännchen bitte erkläre mir genauer, was falsch darin ist? Außerdem verstehe ich nicht, was ein Txman ist, welches du ständig erwähnst.

---

Wenn du Mathematiker bist, kommst du da sicher von selbst drauf. Ansonsten zitiere ich dich gerne auch da:

Helfen heißt aber auch nicht den Kindern hier alle Arbeit abzunehmen. Sie müssen auch selbst etwas leisten.

In diesem Sinne: recherchiere selbst.

Answer 4

2)

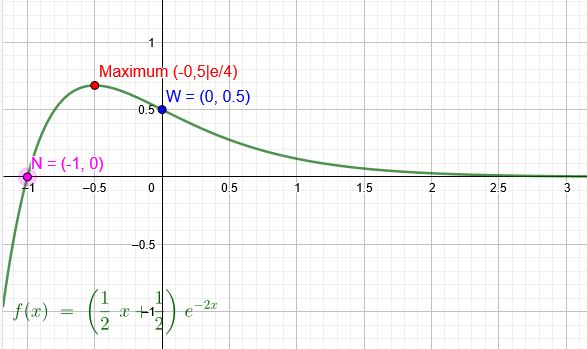
\( f(x)=(\frac{1}{2} x+\frac{1}{2}) \cdot e^{-2 x} \)

Nullstellen:

\( \frac{1}{2} x+\frac{1}{2} =0 \)

\(x=-1\)

\(e^{-2 x}≠0 \)

Exrempunkte:

Ableitung mit der Produktregel:

\([u\cdot v]'=u'v+uv'\)

\( u=\frac{1}{2} x+\frac{1}{2} \) →  \( u'=\frac{1}{2}  \)

\( v=e^{-2 x} \)    → \( v'=-2e^{-2 x} \)

\( f'(x)=\frac{1}{2} \cdot e^{-2 x}+(\frac{1}{2} x+\frac{1}{2}) \cdot ( -2)\cdot e^{-2 x} \)

\( f'(x)=\frac{1}{2} \cdot e^{-2 x}- (x+1) \cdot e^{-2 x} \)

\( f'(x)= e^{-2 x}(-\frac{1}{2} - x)  \)

\( -\frac{1}{2} - x=0  \)

\(x=\red{ -\frac{1}{2}}   \)      \( f(-\frac{1}{2} )=[\frac{1}{2} \cdot (-\frac{1}{2} )  +\frac{1}{2}] \cdot e^{-2 \cdot (-\frac{1}{2} ) }=\frac{e}{4} \)

\( f'(x)= e^{-2 x}(-\frac{1}{2} - x) =\frac{-\frac{1}{2} - x}{ e^{2 x}} \)

Ableitung mit der Quotientenregel:

\([\frac{Z}{N}]'=\frac{Z'N-ZN'}{N^2}\)

\(Z=-\frac{1}{2} - x\)→ \(Z'=-1\)        \(  N= e^{2 x}\)  → \(  N'= 2e^{2 x}\)

\( f''(x)=\frac{(-1) \cdot e^{2 x}-(-\frac{1}{2} - x) \cdot 2e^{2 x} }{(e^{2 x})^2}\)

\( f''(x)=\frac{(-1) \cdot e^{2 x}+(1 +2x) \cdot e^{2 x} }{(e^{2 x})^2}\)

Jetzt braucht man die Kürzungsregel: "Aus Differenzen und aus Summen kürzen nur die Dummen."  nicht beachten.

\( f''(x)=\frac{2x }{e^{2 x}}\)

Art des Extrempunktes:

\( f''(\red{ -\frac{1}{2}} )=\frac{2(\red{ -\frac{1}{2}} ) }{e^{2 (\red{ -\frac{1}{2}} )}}=\frac{-1}{e^{-1}}=-e<0\) Maximum

Wendepunkte:

\( \frac{2x }{e^{2 x}}=0\)

\(x=0\)      \( f(0)=\frac{1}{2} \cdot e^{0}=\frac{1}{2} \),  weil   \( e^{0}=1\)

Comments

wow, vielen dank

---

Jetzt braucht man die Kürzungsregel: "Aus Differenzen und aus Summen kürzen nur die Dummen."  nicht beachten.

Eine weitere didaktische Katastrophe.

The same procedure as (most) every bullshit...

Die Regel gilt immer noch. Leider hast du es nicht hinbekommen dem Fragesteller mitzuteilen, dass erst durch Ausklammern die Summe in eine Produktform umgewandelt wird, wodurch das Kürzen eines gemeinsamen FAKTORS möglich wird.

---

dass erst durch Ausklammern .... möglich wird

warum sollte man einen gemeinsamen Faktor aller Summanden einer Summe nicht einfach rauskürzen?

Es ist doch bei dir und anderen geradezu erwünscht, wenn dem FS ggf. etwas zum Nachfragen übrig bleibt.

Warum also die Lösung komplettieren?

---

\(3x^2+12x-15=0\)

Hier schreibt man ja auch nicht:

\(3 \cdot (x^2+4x-5)=0|:3\)

\(x^2+4x-5=0\)

Sondern kürzt gleich mit der 3.

---

Ganz schlechtes Beispiel.

Das didaktische Problem besteht darin, dass das Kürzen aus einer Summe, wie du es getan hast, auf dem ersten Blick deiner zitierten Regel (wobei ich das eher einen Merksatz nennen würde) widerspricht. Andererseits hast du aber gesagt, dass man das nicht beachten muss. Hier wäre es - der Vollständigkeit halber - aber sicherlich sinnvoll gewesen, zu erwähnen, wieso man in diesem Fall dann doch aus einer Summe kürzen darf, obwohl die "Regel" es verbietet. Solche Widersprüche führen aber nicht selten zu Verständnisproblemen.

Es ist doch bei dir und anderen geradezu erwünscht, wenn dem FS ggf. etwas zum Nachfragen übrig bleibt.

Warum also die Lösung komplettieren?

Es gibt einen Unterschied zwischen "Ansätze vorgeben" und "Aufgabe vorrechnen". Wenn man beim Vorrechnen relevante Schritte weglässt, kann das durchaus problematisch sein und ist dann weniger hilfreich. Vor allem, wenn man dann noch entsprechende "Regeln" zitiert und ihnen im nächsten Schritt scheinbar widerspricht.

Die meisten Lösungswege werden stumpf abgeschrieben, ohne zu hinterfragen. Daher ist Variante 1 sinnvoller.

---

Hieße es \( f''(x)=\frac{(-1) \cdot e^{2 x}+(1 +2x) \cdot e^{2 x}+x^2 }{(e^{2 x})^2}\)

statt \( f''(x)=\frac{(-1) \cdot e^{2 x}+(1 +2x) \cdot e^{2 x} }{(e^{2 x})^2}\)

Dann wäre selbstverständlich das Kürzen verboten.

Also immer genau schauen.

---

Die Problematik kann man übrigens vollkommen vermeiden, indem man einfach die Produktregel nutzt.