Gegeben ist die Logistische Differentialgleichung:
\( \frac{\mathrm{d}}{\mathrm{d} t} x=a x-b x^{2} \text { mit } a, b>0 \text { . } \)
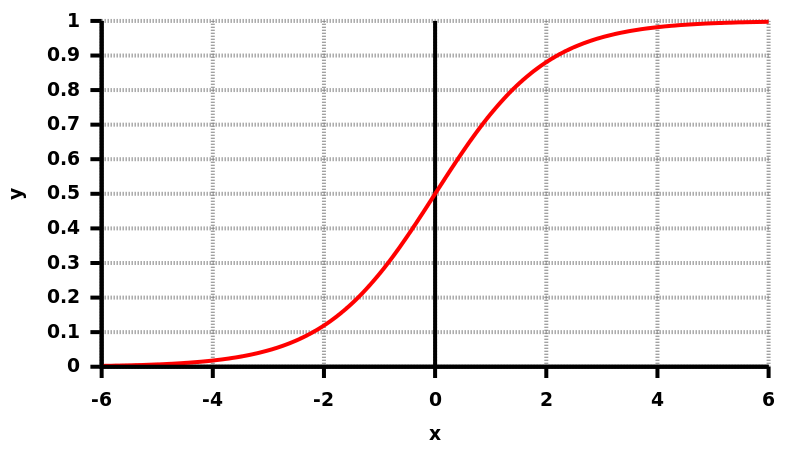
a) Skizzieren Sie die Funktion \( f(x)=a x-b x^{2} \) für \( a=1 \) und \( b=1 \). Machen Sie sich klar, warum die Logistische Differentialgleichung ein gutes Modell für Populationen mit begrenztem Wachstum darstellt.
b) Zusatzaufgabe: Lösen Sie nun diese Differentialgleichung für beliebige Anfangspopulationen,
d.h. zur Zeit \( t_{0} \) sei \( x\left(t_{0}\right)=x_{0} \) und \( x_{0}>0 \). Formen Sie dazu die Gleichung durch Trennung der Variablen in einen Integralausdruck um. Berechnen Sie das Integral über \( x \) mit Hilfe der Substitution \( y=\frac{1}{x} \). Was erhalten Sie damit letztendlich für \( x(t) ? \)
c) Zusatzaufgabe: Wie verhält sich die Funktion \( x(t) \) für große Zeiten \( t \rightarrow \infty ? \) Was ergibt sich für den Grenzfall \( b=0 \) ?
Ansatz:
Mein Vorschlag:

Die Zusatzaufgaben b und c sind nicht so wichtig, aber a). Ich muss die Aufgaben (ich habe noch 4 weitere Aufgaben im Forum reingestellt) bis morgen abgegeben haben. Habe ich oben den richtigen Ansatz gemacht? Ich habe für a und b 1 eingesetzt. Daraus folgt: x-x², wie oben gezeichnet. Ist das richtig?
Die logistische Funktion, wie sie sich aus der diskreten logistischen Gleichung ergibt, beschreibt den Zusammenhang zwischen der verstreichenden Zeit und einem Wachstum, beispielsweise einer idealen Bakterienpopulation. Hierzu wird das Modell des exponentiellen Wachstums modifiziert durch eine sich mit dem Wachstum verbrauchende Ressource – die Idee dahinter ist also etwa ein Bakteriennährboden begrenzter Größe. (Wikipedia)