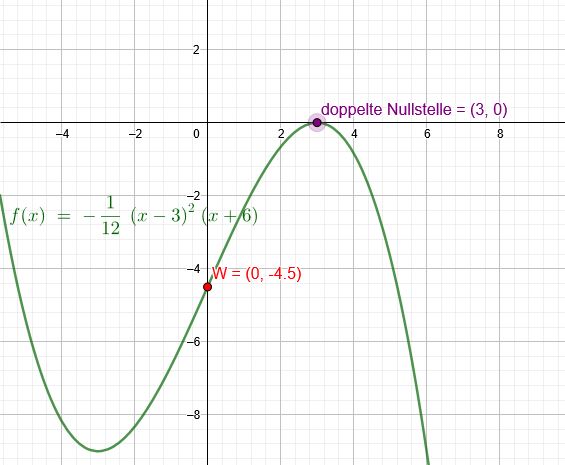
Funktion 3. Grad diese hat eine doppelte NST bei \(x_1,_2 = 3\) und Wendepunkt W(0|-4,5)
Linearform der kubischen Parabel:
\(f(x)=a*(x-3)^2*(x-N) \)
\(W(0|-4,5)\)
\(f(0)=a*(0-3)^2*(0-N)=-9a*N=-4,5 \) → \(a=\frac{1}{2N} \)
\(f(x)=\frac{1}{2N}*[(x-3)^2*(x-N)] \)
\(f´(x)=\frac{1}{2N}*[(2x-6)*(x-N)+(x-3)^2] \)
\(f´´(x)=\frac{1}{2N}*[(2x-2N)+(2x-6)+(2x-6)] \)
\(f´´(0)=\frac{1}{2N}*[-2N-6-6]=\frac{1}{2N}*[-2N-12]=0 \) →\(N=-6\) \(a=-\frac{1}{12} \)
\(f(x)=-\frac{1}{12} *(x-3)^2*(x+6) \)