Funktion Dritten Gerades aufstellen durch Extrema und Wendepunkt

Question

Ich denke mir jetzt einfach mal eine aus..hoffe das geht so:)

Tiefpunkt T(2|4) und dem Wendepunk (1|0)

Wie die Funktionsgleichung aussieht, weiß ich mittlerweile auch :D

f(x)= ax³+bx²+cx+d

Ich leite das 3mal ab... vielleicht braucht man das ja :)

f'(x)= 3ax²+2bx+c

f''(x)= 6ax+2b

f'''(x)= 6a

so und jetzt? :)

Answer 1

Na, das ging ja schnell :-D

 

Der Graph der Funktion geht durch (2|4), also

I. f(2) = 4 = 8a + 4b + 2c + d

Dort ist ein Tiefpunkt, also ist dort die 1. Ableitung = 0:

II. f'(2) = 0 = 12a + 4b + c

Die Funktion geht durch (1|0), also

III. f(1) = 0 = a + b + c + d

Sie hat dort einen Wendepunkt, also

IV. f''(1) = 0 = 6a + 2b

4 Unbekannte, 4 Gleichungen :-)

Es ergibt sich

a = -2

b = 6

c = 0

d = -4

Die Funktionsgleichung lautet also

f(x) = -2x³ + 6x² - 4

Haut leider mit Deinem "Tiefpunkt" (2|4) nicht hin, ist aber immerhin ein Extremum:

 

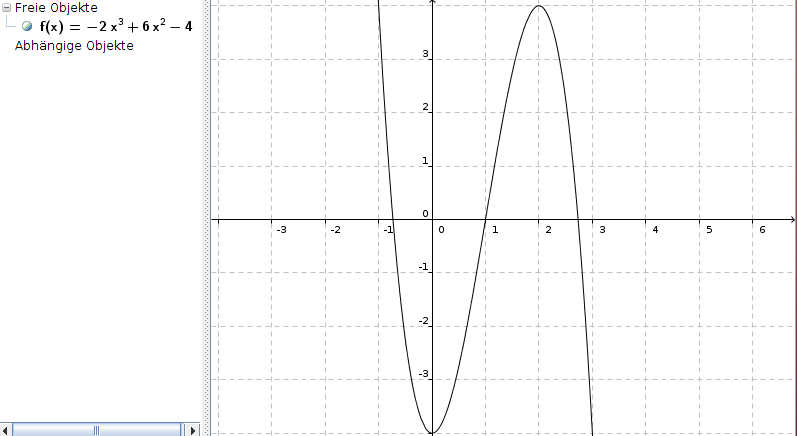
Lieben Gruß

Andreas

Comments

Hallo Andreas :)

Dankeschön für die Antwort!

Ich werde mir das mal später in Ruhe anschauen :)

Answer 2

Hi,

Du hast eine Funktion mit 4 Unbekannten, also brauchst Du auch 4 Bedingungen. Z.B. Nulldurchgang oder einen zweiten Tief- / Hochpunkt. Dann kannst Du die Koeffizienten Deines Polynom berechnen.