Hallo Matheexperts,
im Bild seht Ihr den Graphen eines Polynoms 4. Grads
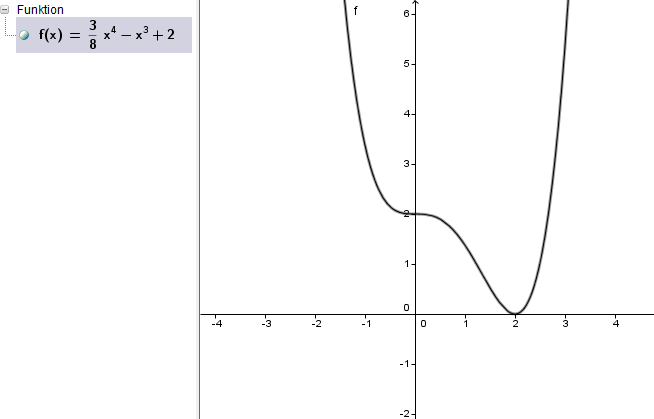
Nun versuche ich die Nullstellen dieses Polynoms mittels Polynomdivision zu finden. Im Internet gibt es dafür Online-Tools, die das für mich erledigen. Als Ergebnis erhalte ich eine Nullstelle bei x=2 und drei Ergebnisse mit imaginären Zahlen.
Nun meine Frage: Wie kann ein Mensch, der noch nichts von imaginären Zahlen weiss (Schüler der 11 Klasse), durch Polynomdivision, pq-Formel, Ausklammern etc. feststellen, dass dieses Polynom nur eine Nullstelle hat?
Vielen Dank für Euere Hilfe
