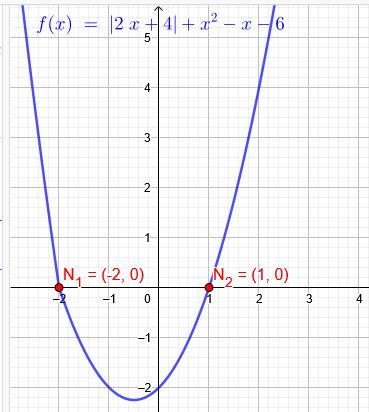
\(|2x + 4| = - (x² - x - 6) \)
\(2*|x + 2| = - [x² - x - 6] \)
Zwischenrechnung:
\( x² - 1*x - 6=0 \)
\( x² - 1*x =6 \)
\( (x - 0,5)^2=6,25 \)
1.)
\(x - 0,5=2,5 \)
\(x_1=3 \)
2.)
\(x - 0,5=-2,5 \)
\(x_2=-2 \)
...............
\(2*|x + 2| = (- 1)*(x-3)*(x+2) |^2 \)
\(4*(x + 2)^2 = (x-3)^2*(x+2)^2 \)
\(4*(x + 2)^2 - (x-3)^2*(x+2)^2 =0 \)
\([(x + 2)^2]*[4 - (x-3)^2]=0 \)
Satz vom Nullprodukt:
1.)
\([(x + 2)^2]=0 \)
\(x=-2 \) Probe, da Quadrieren keine Äqivalenzumformung ist:
\(|2*(-2) + 4| = - ((-2)^2 +2 - 6) \)
\(0 = - (4 +2 - 6) \) stimmt
2.)
\([4 - (x-3)^2]=0 \)
\([ (x-3)^2=4 \)
A) \([ x-3=2 \)
\([ x=5 \)
\(|2*5+ 4| = - (25 - 5 - 6) \) stimmt nicht
B) \([ x-3=-2 \)
\( x=1 \)
\(|2 + 4| = - (1 - 1 - 6) \) stimmt