So, wieder da ;).
Eine Nullstelle hast Du doch direkt zu x1 = 1 erraten/bestimmt.
Daraus hast Du ein Polynom vierten Grades erhalten und diese mit Substitution gelöst. Da hast Du erhalten
z1,2 = 1 erhalten.
Eine Resubstitution ergibt:
x2,3 = -1 und x4,5 = 1
Du hast also fünf Nullstellen. Das sieht dann so aus:
(x-1)(x-1)(x-1)(x+1)(x+1) = (x-1)^3(x+1)^2
Nun kannst Du anhand der sogenannten Vielfachheit bestimmen, ob ein Vorzeichenwechsel an den Nullstellen vorliegt oder nicht (nur dort kann das Vorzeichen sich ändern).
Für x = -1 haben wir eine doppelte Nullstelle (sieht man an (x+1)^2) -> kein Vorzeichenwechsel.
Für x = 1 haben wir eine dreifache Nullstelle -> Vorzeichenwechsel.
Wir haben also nur bei x = 1 einen Vorzeichenwechsel.
Schauen wir mal was wir bei p(0) haben: p(0) = -1. Sind also negativ.
Folglich:
Für x ≤ 1 ist P(x) ≤ 0
Für x ≥ 1 ist P(x) ≥ 0
Zur Veranschaulichung:
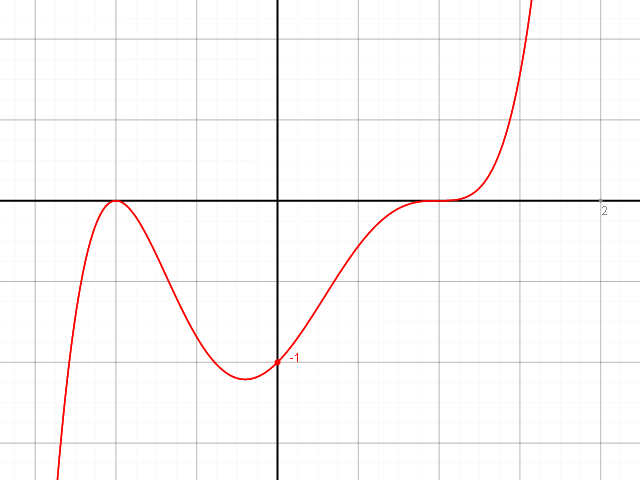
Schaut gut aus, was wir gesagt/gemacht haben :).