Bestimme den Punkt P, in dem die Tangente die Parabel berührt

Question

Gegeben ist die Funktion f mit f(x)= 4x² und die Steigung m einer Tangente an die Parabel. Bestimme den Punkt P, in dem die Tangente die Parabel berührt.

m=2

Answer 1

Dir ist die Steigung der Tangente bekannt. Nun gibt die erste Ableitung die Steigung in einem Punkt an.

f'(x) = 8x

f'(x) = 8x = 2   |:8

x  = 2/8 = 1/4

x-Wert ist damit gefunden. y-Wert ergibt sich durch einsetzen in f(x) zu f(1/4) = 4*(1/4)^2 = 1/4

Der Berührpunkt ist damit P(1/4|1/4).

Grüße

Comments

Dankeschöön für die schnelle Antwort. Aber ableitung hatten wir bis jetzt noch nicht. Gibt es dafür eine andere Möglichkeit?

---

kennst Du den Differenzenquotienten? Das ist die Vorstufe zur Ableitung, mit der würde es auch funktionieren.

Letztlich könnte man es noch graphisch lösen (relativ ungenau). Mehr würde mir spontan nicht an Alternativen einfallen ;).

Answer 2

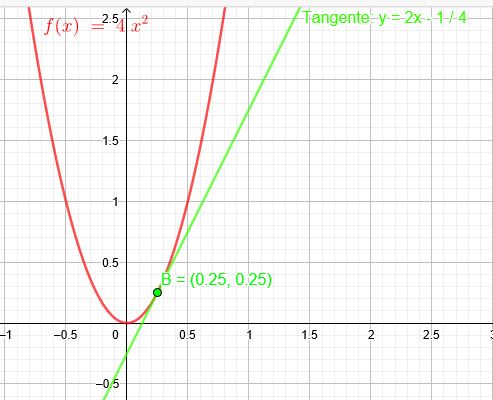
Gegeben ist die Funktion f mit \(f(x)= 4x^2\) und die Steigung \(m=2\) einer Tangente an die Parabel. Bestimme den Punkt P, in dem die Tangente die Parabel berührt.

Möglicher Weg ohne Ableitung:

\(y=2x+n\) ist eine zueinander parallele Geradenschar. Diese Schar nun zum Schnitt mit der Parabel bringen:

\( 4x^2=2x+n |-2x\)

\( 4x^2-2x=n |:4\)

\( x^2-\frac{2}{4}x=\frac{n}{4} \)    quadratische Ergänzung:

\( x^2-\frac{2}{4}x+(\frac{1}{4})^2=\frac{n}{4} +(\frac{1}{4})^2\)    2.Binom:

\( (x-\frac{1}{4})^2=\frac{n}{4} +(\frac{1}{4})^2 |±\sqrt{~~}\)

\(x_1,_2=\red{\frac{1}{4}}±\sqrt{\frac{n}{4} +\frac{1}{16}}\)

Eine Tangente liegt dann vor, wenn die Diskriminante \(=0\):

\(\frac{n}{4} +\frac{1}{16}=0\)

\(n=-\frac{1}{4}\)

Die Tangente hat so die Gleichung  \(y=2x-\frac{1}{4}\)

Die Berührstelle ist nun \(x=\red{\frac{1}{4}}\)

\(y(\red{\frac{1}{4}})=2\cdot\red{\frac{1}{4}}-\frac{1}{4}=\frac{1}{4}\)

Koordinaten des Berührpunktes: B\((\frac{1}{4}|\frac{1}{4})\)

Comments

Du erkennst, dass der Passus

Eine Tangente liegt dann vor, wenn die Diskriminante \(=0\):
\(\frac{n}{4} +\frac{1}{16}=0\)
\(n=-\frac{1}{4}\)
Die Tangente hat so die Gleichung  \(y=2x-\frac{1}{4}\)

hier komplett überflüssig ist?

---

Faule Schüler können bei Bedarf auch die Bestimmung von n und der Tagente weglassen und gleich den Punkt berechnen, nach dem ja nur gefragt wurde.

Weiterhin empfehle ich für Schüler meist die Benutzung einer Lösungsformel statt quadratischer Ergänzung.

---

Immerhin war der Ansatz sinnvoll und die Lösung hatte keine Fehler - das sind doch Fortschritte.

---

@ MC: Wie kann man den Berührpunkt bestimmen, ohne die Tangente zu bestimmen?

---

Es reicht doch, die einzige Schnittstelle zwischen Gerade und Parabel zu bestimmen. Dafür braucht es keine explizite Angabe der Tangentengleichung, siehe den rot markierten Wert in der Lösung der Gleichung und den Kommentar von abakus.

---

Naja. Wenn man die Schnittstelle hat - wie will man die bestimmen, ohne die Tangente anzusetzen? - Und die Steigung, dann hat man auch die Tangente.

---

Klar musst du den Ansatz mit der Tangente machen, aber eine Gleichung dafür muss eben nicht explizit bestimmt werden. Und das war auch die Aussage von MC: Die Berechnung von \(n\) und damit die Angabe der Tangentengleichung weglassen.

Ganz ohne Tangente geht es natürlich, indem man direkt mit der Ableitung arbeitet.

---

Wenn man diese einfache Aufgabe als Mathematik Aufgabe ernst nimmt, dann gehört zur Beantwortung auch, dass es genau ein solches n gibt ....

Mal ehrlich: Ich habe keine Ahnung von Schul Didaktik. Aber ich finde es schon sehr spitzfindig die Angabe der Tangente zu monieren, wenn diese de facto schon bestimmt ist. Meine Vorstellung von Mathematik Unterricht wäre, SuS zu gut begründeten abgerundeten Sinn-VOLLEN Lösungsdarstellungen anzuhalten.