Hier eine ganz allgemeine Lösung
Aus einem Rechteck mit den Seiten a und b soll durch herausschneiden von Quadraten mit der Seitenlänge x ein oben offener Quader mit max. Volumen hergestellt werden.
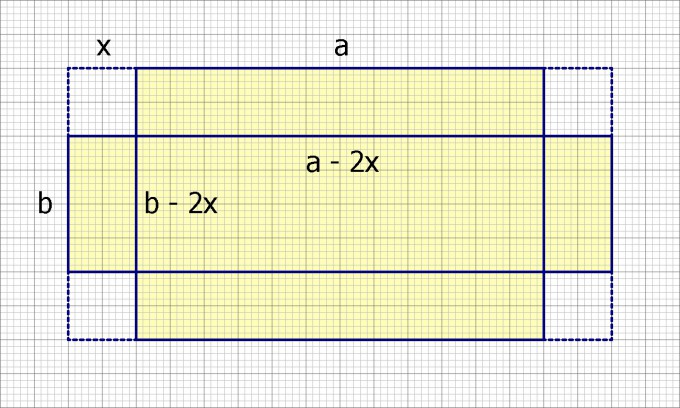
1. Die zu maximierende Zielfunktion aufstellen.
V = (a - 2·x)·(b - 2·x)·x = 4·x^3 - 2·a·x^2 - 2·b·x^2 + a·b·x
2. Damit die Zielfunktion ein Maximum hat muss die Ableitung Null werden.
V' = 12·x^2 - (4·a + 4·b)·x + a·b = 0
x = (-b - √(b^2 - 4·a·c))/(2·a)
x = ((4·a + 4·b) - √((4·a + 4·b)^2 - 4·(12)·(a·b)))/(2·(12))
x = (a + b)/6 - √(a^2 - a·b + b^2)/6