Ein Industriebetrieb fertigt gemäß nebenstehendem Verflechtungsgraphen aus den Ausgangsprodukten \( A_{1}, A_{2} \) und \( A_{3} \) zunächst die Zwischenprodukte \( Z_{1}, Z_{2} \) und \( Z_{3} \). Aus diesen drei Zwischenprodukten werden dann die beiden Endprodukte \( E_{1} \) und \( E_{2} \) zusammengefūgt.
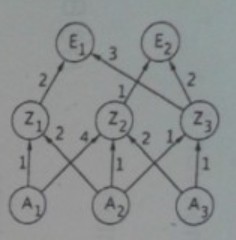
Die Verflechtungsmatrizen AZ bzw. ZE geben an, wie viel Stūck von den Ausgangsprodukten \( A_{1}, A_{2} \) und \( A_{3} \) zur Produktion je eines Stūcks der Zwischenprodukte \( Z_{1}, Z_{2} \) und \( Z_{3} \), beziehungsweise wie viel Stūck von den Zwischenprodukten zur Produktion je eines Stûcks der Endprodukte \( E_{1} \) und \( E_{2} \) benötigt werden.
Geben Sie die Matrizen AZ und ZE an.
Berechnen Sie, wie viele Ausgangsprodukte benötigt werden, damit eine Bestellung über 500 Endprodukte \( \mathrm{E}_{1} \) und 400 Endprodukte \( \mathrm{E}_{2} \) bearbeitet werden kann.
Für eine Bestellung an Endprodukten wurden 3300 Stūck von \( A_{1}, 4400 \) Stück von \( A_{2} \) und 3650 Stück von \( \mathrm{A}_{3} \) bereitgestellt. Leider sind die Bestellunterlagen verloren gegangen.
Bestimmen Sie, wie die Bestellung an Endprodukten lautete.
Ansatz/Problem:
Es hackt bei dem letzen Aufgabenteil, bei welchem die Bestellung an Produkten ermittelt werden muss. Bis jetzt habe ich: AE mal Bestellungsvektor = Vektor, der die Menge an Ausgangsstoffen für die Bestellung an Endprodukten angibt (Produktionsvektor): Bestellungsvektor = AE-1 mal Produktionsvektor, doch das geht nicht.
Dann hab ich es mit der Direktbedarfsmatrix probiert, aber da entspricht der Bestellungsvektor dem Produktionsvektor.