Berechnen Sie den Break-Even-Point (anhand von zwei Funktionen)

Question

Aufgabe:

Die Kostenfunktion für die Produktionsmenge $x$ eines Gutes sei gegeben diurch: $K(x)=\frac{x^{2}}{24}+\frac{x}{12}+\frac{14}{3}$ mit $\mathbb{D}(K)=[0,12]$. Die Preis-Absatz-Funktion $p(x)=-\frac{x}{4}+3$ sei ebenso auf $[0,12]$ definiert.

Berechnen Sie den Break-Even-Point.

Ansatz:

Es handelt sich um einen Break-Even Point, den man anhand zweier Funktionen finden muss.

Das Problem ist, dass ich das normalerweise mit dem Schnittpunkt mache. Diese beiden Funktionen schneiden sich aber nicht. Wie geht man da vor? Das ist mir noch nie zuvorgekommen.

PS: K ist auch [0;12]

Comments

Der Gewinn ist die Differenz aus den Erlösen, also hier der Preis, minus den Kosten.

Also solltest du vielleicht die zwei Funktionen voneinander abziehen und die daraus resultierende Gewinnfunktion 0 setzen, da der Gewinn an der Break-Even Menge 0 ergibt.

Answer 1

Breakeven-Point wäre interessant für den Vergleich von Erlös- und Gesamtkostenfunktion. Du vergleichst hier aber Preis- mit Gesamtkostenfunktion.

Überleg dir erstmal wie Erlös und Preisfunktion zusammenhängen.

Gruß

Answer 2

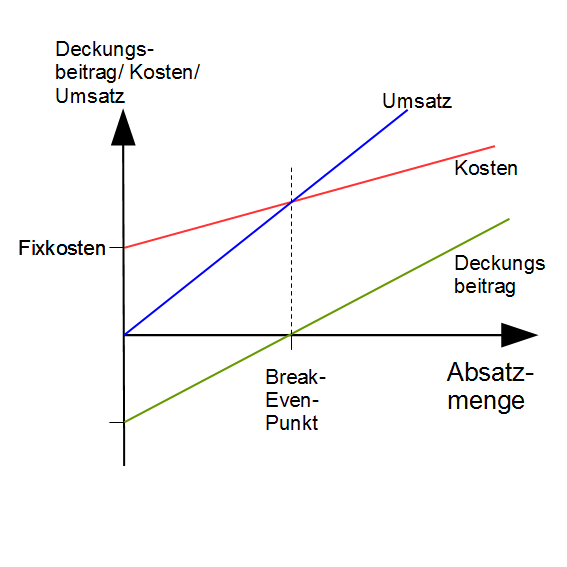
Der Break Even Punkt ist dort, wo gilt: Kosten = Umsatz.

Der Break-Even-Point (oder auch Gewinnschwelle bzw. Break-Even-Punkt) gibt Auskunft darüber, wie viel man von einem Produkt (in einem bestimmten Zeitraum) verkaufen muss, um einen Gewinn zu erzielen.

Beispiel Berechnung Break-Even-Point

Das Unternehmen A möchte wissen, wie viel es von seinem Produkt P verkaufen muss, um rentabel zu sein.

Pro Jahr fallen fixe Kosten in Höhe von 1000 GE an.
Die variablen Kosten liegen pro Stück bei 5 GE.
Der angepeilte Preis liegt pro Stück bei 9 GE.
BEM = 1000 / (9-5)

BEM = 250

Wenn das Unternehmen 250 Stück verkauft hat, gleichen sich Kosten und Umsatz aus Hier liegt der Break-Even-Point. Schafft es das Unternehmen A, mehr abzusetzen, erzielt es einen Gewinn. Gelingt es dem Unternehmen nicht, die 250 Stück zu verkaufen, kann es die Fixkosten nicht decken.

Die Kostenfunktion hast du gegeben mit K(X).

Den Umsatz musst du dir selbst "zusammenbasteln" p(x) + x

Also: Preis * Menge.

Dann stellst du die Formel auf, indem du K(x) = p(x) + x gleichsetzt.

Du wirst sehen, dass eine quadratische Gleichung entsteht, die du Lösen musst. Du erhältst dann die Werte für x.

Zur Kontrolle: x1 = 2

x2 = 8

Weitere Informationen zum Break Even Point mit Beispielen, Aufgaben und Rechner findest du hier: https://www.preissetzung.de/break-even-point/