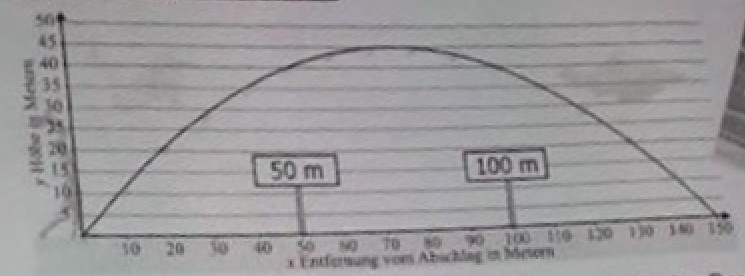
Beim Golf kann die Flugbahn des Balles annähernd durch eine Parabel beschrieben werden.
a) Welche Höhe erreicht der Ball in dem oben dargestellten Schlag?
b) Wie weit fliegt der Golfball oben?
c) Eine der folgenden Funktionsgleichungen gehört zur dargestellten Parabel, kreuze an:
(A) \( y=-0.008 x^{2}+1.2 x \)
(B) \( y=-0.05 x \)
(C) \( y=0,18 x^{2} \)
Begründe, warum die anderen Funktionsgleichungen nicht zur Parabel gehören können.
d) Eine andere Flugbahn kann durch die Gleichung \( y=-0,002 x^{2}+0,5 x \) beschrieben werden. In welcher Höhe befindet sich der Golfball jetzt über der 50 m-Markerung? Notiere deine Rechnung. Wie weit fiegt der Goltball jetzt? Notiere deine Rechnung!
e) Ein anderer Ball, dessen Flugbahn ebenfalls durch eine Parabel beschieben werden kann, erreicht seine maximale Höhe erst über der 100 m-Markierung. In welcher Entfernung vom Abschlag landet er? Begründe deine Antwort.