Gegeben ist ein Kegel mit dem Neigungswinkel von 30° und einem Umfang von 24 m.
Wie berechnet man jetzt das Volumen in m³?
Da du nichts Genaueres schreibst, nehme ich an, dass es sich um einen geraden Kreiskegel handelt.
Die Volumenformel für Kegel ist V = 1/3 * G*h. G: Grundfläche, h: Höhe.
Mit Umfang ist hier Umfang des Grundkreises gemeint. u = 2 pi r. Wobei r: Radius.
|dividiere durch 2 pi.
u / (2*pi) = r.
G = pi*r^2 |r einsetzen
G = pi * (u/(2*pi))^2 | Potenzgesetze anwenden
= pi* (u^2 / (4*pi^2) | alles auf einen Bruchstrich; kürzen
= u^2 / (4*pi)
Wenn du einen Längsschnitt zeichnest, siehst du 2 rechtwinklige Dreiecke mit den Seiten r, h und Seitenlinie, Winkel 30°. Dort gilt von 30° aus gesehen (Gegenkathete h) / (Ankathete r) = tan 30°
h : r = tan 30° = 1/√3 | *r
h = r* 1/√3 | r einsetzen
h = u / (2*pi) * 1/√3 | auf einen Bruchstrich bringen
= u / (2*pi*√3)
Jetzt mit G und u in die Formel für V und das noch vereinfachen
V = 1/3 * (u^2 / (4*pi)) * (u / (2pi√3))
= u^3 / (24*√3 * pi^2 )
Nun u=24m einsetzen
V = 24^3 / (24*√3*pi^2 ) |kürzen
V = 24^2 / (√3*pi^2) = 33.695m^3
Schreib das jetzt noch mit richtigen Bruchstrichen ab und rechne nach. Das ist jetzt ziemlich lang und unübersichtlich geworden und hat möglicherweise noch Rechenfehler drinn.
Ich muss dir nun noch mit dem Pythagoras zeigen, dass h = r / √3 ist. Vgl Zeichnung:
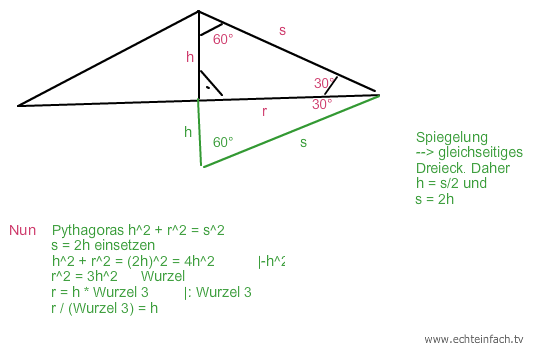
Nun kannst du den Teil mit tan 30° oben vergessen.