Suche Kreise, welche durch die Punkte P(8/-6) und Q(4/-2) gehen und die y-Achse berühren!

Question

Der Kreis (mit allen seinen Geheimnissen)

Ermittle die Gleichungen jener Kreise, welche durch die Punkte P(8/-6) und Q(4/-2) geht und die Y-Achse berühren!

bitte mit Rechenschritte

     danke

Answer 1

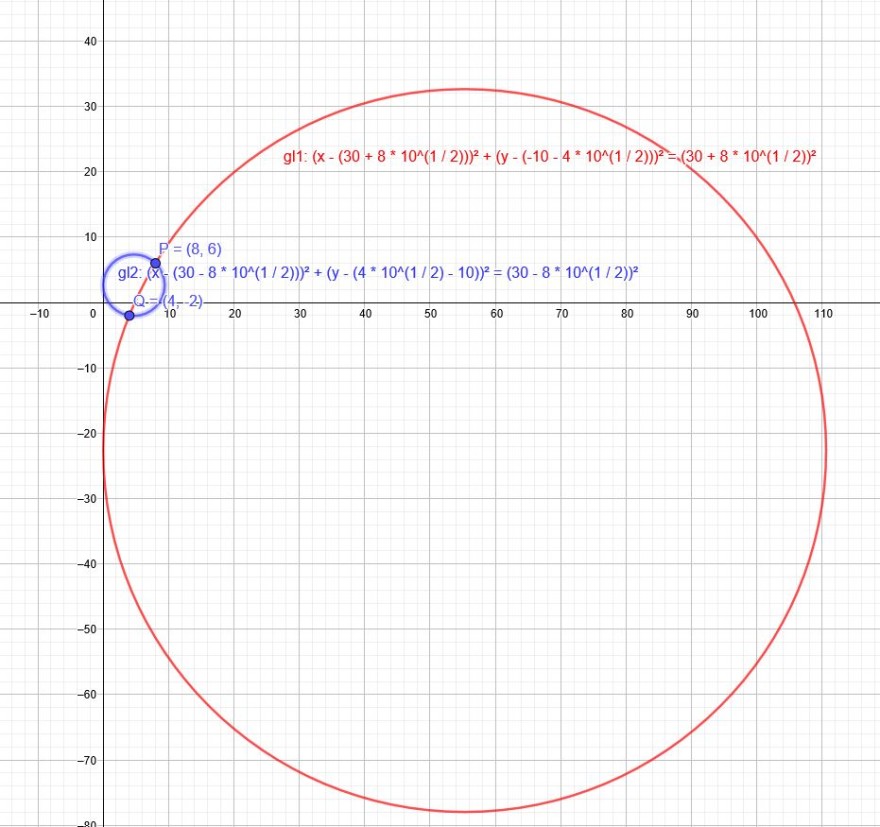
Ermittle die Gleichungen jener Kreise, welche durch die Punkte \(P(8|-6)\) und \(Q(4|-2)\) geht und die y-Achse berühren!

\((x-x_M)^2+(y-y_M)^2=r^2\)

Berührung der y-Achse \(x_M=r\):

1.)

\((x-r)^2+(y-y_M)^2=r^2\)

\(P(8|-6)\)

2.)

\((8-r)^2+(-6-y_M)^2=r^2\)→  \(100-16r-12y_M+y_M^2=0\)→  \(16r=100-12y_M+y_M^2\)

\(Q(4|-2)\):

3.)

\((4-r)^2+(-2-y_M)^2=r^2\)→ \(20-8r+4y_M+y_M^2=0\) → \(16r=40+8y_M+2y_M^2\)

2.)=3.)

\(100-12y_M+y_M^2=40+8y_M+2y_M^2\)

1.) \(y_M=-10-4\sqrt{10} \)      \(16r=40+8(-10-4\sqrt{10})+2(-10-4\sqrt{10}) ^2\)

 \(r=x_M=30+8\sqrt{10}\)

2.) \(y_M=4\sqrt{10}-10 \)       \(16r=100-12(4\sqrt{10}-10)+(4\sqrt{10}-10)^2\)     

 \(r=x_M=30-8\sqrt{10}\)

Kreis 1.)   \((x-(30+8\sqrt{10}))^2+(y-(-10-4\sqrt{10}))^2=(30+8\sqrt{10})^2\)

Kreis 2.)   \((x-(30-8\sqrt{10}))^2+(y-(4\sqrt{10}-10) )^2=(30-8\sqrt{10})^2\)

Comments

P ist falsch.

---

Das ist relativ irrelevant, da er als erster erkannt hat, dass es zwei mögliche Lösungen gibt – wenn auch erst nach 11 Jahren.

---

P ist falsch.

Das stimmt! Habe mich verguckt. Der aufgezeigte Weg führt auch zu 2 Kreisen.

---

Wen's interessiert: die Mittelpunkte \(M_1(20|10)\) und \(M_2(4|-6)\) der gesuchten Kreise sind die Schnittpunkte zweier Parabeln, die sich aus jeweils einen der Punkte P und Q als Brennpunkt und der Y-Achse als deren gemeinsame Leitlinie (Leitgerade) ergeben.

bitte mit Rechenschritte

... die Rechnerei wird überbewertet.

Answer 2

Mach dir dazu doch einfach eine Skizze

 

Du hast die Punkte p und q und kannst damit die Mittelsenkrechte bestimmen, auf denen der Kreismittelpunkt liegt. Dann suchst du einen Punkt dieser Geraden der zur y Achse den Gleichen Abstand hat wie zu einem der Punkte P und Q.

Als Ergebnis solltest du M(4|-6) für den Kreismittelpunkt bekommen. Die x Koordinate ist dabei gleichzeitig der Radius, weil die y-Achse ja nur berührt wird.

 

Comments

Also du solltest auf folgende Mittelsenkrechte kommen:

y = x - 10

Das gibt also die Punkte K(x | x - 10) auf dem Kreis

Abstand von K(x | x - 10) zu P(8|-6) ist gleich dem Abstand zur y-Achse (x)

(x - 8)^2 + (x - 10 - (-6))^2 = x^2
2·x^2 - 24·x + 80 = x^2
x = 20 und y 20 - 10 = 10
x = 4 und y = 4 - 10 = -6

Damit gibt das zwei Kreise, die die Bedingung erfüllen

K1: (x - 20)^2 + (y - 10)^2 = 20^2
K2: (x - 4)^2 + (y + 6)^2 = 4^2

---

wie kommen sie auf y = x - 10

danke

---

wie sind sie auf y=x-10 gekommen

---

Ich habe diesen Teil gerade noch vorgerechnet.

---

P(8/-6) und Q(4/-2)

Du Berechnest den Punkt zwischen P und Q

1/2 * ((8 | -6) + (4 | -2)) = (6 | -4)

Jetzt berechnet man die Steigung zwischen P und Q

m1 = (y1 - y2) / (x1 - x2) = (-6 - (-2)) / (8 - 4) = -4/4 = -1

Senkrecht zur Steigung 1 ist die Steigung m2 = 1

Nun stellt man die Gerade in der Punkt Steigungs Form auf

y = m * (x - Px) + Py = 1 * (x - 6) + (-4) = x - 10

---

Man kann die Mittelsenkrechte aber auch aus der Zeichnung ablesen. Das geht bei den Geraden Werten ja recht einfach.

Answer 3

Hier eine ausführliche Berechnung der Mittelsenkrechten:

P(8/-6) und Q(4/-2) 

Koordinaten der gegebenen Punkte wie folgt einsetzen:

Mittelpunkt

M_PQ ( (4+8)/2 | (-6-2)/2) = M_PQ( 6 | -4)

Steigung PQ: m = (-6 -(-2) ) / (8-4) = -4 / 4 = -1

Senkrecht dazu m₂ = - 1/m = -1/ ( -1) = 1

Gleichung Mittelsenkrechte.

Ansatz y = 1*x + q

M_PQ einsetzen.

-4 = 6 + q     |-6

-10 = q

Also Gleichung der Mittelsenkrechten: y = x -10.

Den Rest kannst du der schönen Skizze und der Rechnung von Mathecoach entnehmen oder nochmals selbst probieren.