Voraussetzungen des Konvergenzsatzes des Newtonverfahrens: Funktion lautet f(x)=2x-e^{-x}

Question

ich habe eine  Funktion

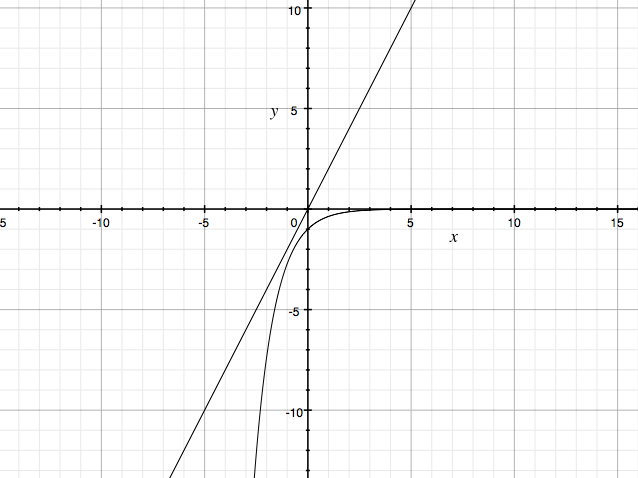
 f(x)=2x-e^{-x}

und muss die Nullstellen mithilfe des n+Newtonverfahrens bestimmen.

Hierbei muss ich überprüfen die Voraussetzungen des Newtonverfahrens. Also die erste Voraussetzung ist Zwischenwertsatz. Ich muss zuerst ein Intervall bestimmen in welchem meine Nullstele möglicherweise liegt.

Ich versuche eine Stelle zu bestimmen (ungefähr)wo die Funktionen f(x)=2x uns f(x)=-e^-x sich schneiden (und das heißt wo die NST der Funktion vorliegt). Aber die schneiden sich nicht. Warum und wie kann ich anhand der Skizze bestimmen , wo die NST vorliegt?

Comments

Funktion lautet f(x)=2x-e^-x

---

Kleiner Fehler.

Du musst die Funktionen auch gleich setzen

g(x)=2x

f(x)=e^{-x}

g(x)=f(x) oder g(x)-f(x)=0

Answer 1

Hi,
wenn die Funktion für die Du die Nullstellen suchst lautet \(f(x)=-e^{-x}-2x \), dann ist es so wie Du sagst, diese Funktion hat keine Nullstellen.