Sätze zu Extrema: Bsp. Wenn f´ an einer Stelle von Null verschieden ist, so kann f dort kein Extremum haben. Richtig?

Question

mache es kurz. Meine Fragen:

 1.was ist ein Extremum

2. Ist es richtig oder falsch?:

wenn der Wert f´ an einer Stelle von Null verschieden ist, so kann f dort kein Extremum haben.

wenn der Wert von f´an einer Stelle Null ist, so hat  f dort ein Extremum

Wenn f´an einer Stelle einen Vorzeichenwechsel hat so hat f dort ein Extremum

Answer 1

Hi,

 

ein Extremum (die Extrema) ist eine besondere Stelle in einem Schaubild. Es handelt sich dabei um Hoch- und Tiefpunkte.

 

Ein Beispiel für ein Extremum. Ein Minimum oder Tiefpunkt.

 

 

wenn der Wert f´ an einer Stelle von Null verschieden ist, so kann f dort kein Extremum haben.

Ja, das ist richtig. Die sogenannte "notwendige Bedingung" verlangt f'(x)=0. Ist das nicht der Fall, gibt es auch kein Extremum.

 

wenn der Wert von f´an einer Stelle Null ist, so hat  f dort ein Extremum

Diesmal ist das nicht ganz richtig. Es könnte sich beispielsweise auch um einen Sattelpunkt handeln.

Bsp.: f(x)=x³

f'(x)=3x²    -> f'(x)=0 -> x=0

Deiner Aussage zur Folge müsste also bei x=0 ein Extremum vorliegen. Schauen wir uns das im Schaubild an:

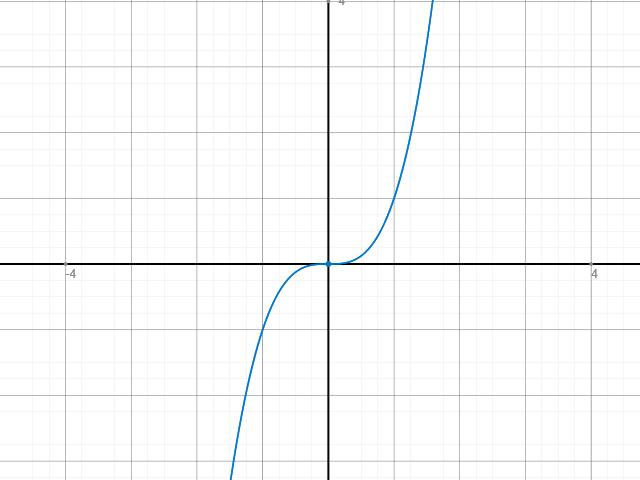
Wir hatten gerade eben gesagt, dass ein Extremum ein Hoch- oder Tiefpunkt ist. Das also in der Nähe der interessanten Stelle kein Wert höher oder niedriger ist. Das ist hier nicht der Fall. Es handelt sich um einen Wendepunkt. Einen Spezialfall davon -> dem Sattelpunkt.

 

Wenn f´an einer Stelle einen Vorzeichenwechsel hat so hat f dort ein Extremum

Das ist wieder richtig.

Comments

Vielen DANK!!!

Ich hätte da noch andere Fragen dazu...auf weitere Antworten würde ich mich sehr freuen.

d) Wenn f´in einem Intervall nur negative Werte hat, so ist f in diesem Intervall streng monoton fallend.

e)wenn f in einem Intervall streng monoton wachsend ist, so hat f´in diesem Intervall nur positive Werte.

f)wenn der Wert von f´an einer Stelle Null ist und der Wert von f´dort von Null verschieden ist, so hat f dort ein Extremum.

g)wenn der wert von f´und von f´ an einer Stelle Null sind, so hat f dort kein Extremum

h) wenn der Wert von f´und von f´an einer Stelle Null sind, so kann f dort ein Extremum haben, muss aber nicht.

Es wäre sehr freundlich, wenn Sie mir alle Fragen (Ob richtig oder nicht) erklären würden, warum es so ist.( eventuell mit Schaubildern.)

Nochmals Danke

---

Ich bin grad nur auf dem Sprung hier und gleich wieder weg.
Ich schaus mir morgen an, oder jemand anderes schaut rein ;).

 

Grüße

Answer 2

1. Als Extremum bezeichnet man eine Stelle des Definitionsbereiches, an dem der Wert einer Funktion einen extremalen Wert annimmt, also entweder einen maximalen oder einen minimalen Wert.

Wenn man den Graphen der Funktion betrachtet dann ist ein lokales Extremum die Stelle, an der der Funktionswert größer bzw. kleiner ist als an allen anderen Stellen in der näheren Umgebung.
Also zum Beispiel der höchste Punkt eines "Hügels".

Ein globales Extremum ist dagegen die Stelle mit dem höchsten/niedrigsten Wert auf dem ganzen Definitionsbereich.

 

2.a) Das ist nur halb richtig. Am Rand des Definitionsbereichs ist f'(x) = 0 nämlich keine notwendige Bedingung. So hat zum Beispiel die Funktion f(x) = x auf dem Intervall [-1, 1] ein lokales und globales Maximum in x=1, aber die erste Ableitung hat dort keine Nullstelle.
Wenn allerdings x innerer Punkt des Definitionsbereichs ist (also nicht am Rand liegt) muss die erste Ableitung zwingend 0 sein.

b) Das ist falsch. f kann an dieser Stelle z.B. auch einen Sattelpunkt haben, wie zum Beispiel

f(x) = x³

an der Stelle x=0.

c) Das ist richtig.