Schnittwinkel Gerade und Kreis k mit: x^2+y^2+10x+2y+6=0. g:3x+y+6=0

Question

Bsp wäre x^2+y^2+10x+2y+6=0. g:3x+y+6=0

Hätte zuerst mal umgestellt damit ich m und r bekomme,um dann mit der hesseschen Abstandsformel zu rechnen

Komme so auf (x+5)^2+(y+1)^2=32

M(-5/-1) r=wurzel 32

Beliebigen Punkt auf g (-3/3)

In die gleichung einsetzten

Betrag von (-5/-1)-(-3/3).1/wurzel10.(3/1)=betrag 1/wurzel10 .(-2/-4).(3/1)=d

Cos q=d/r

Wenn ich dann einsetze in die formel komme ich auf eine winkel mit 55 und nicht laut lösung 45 grad :(

Comments

Warum bestimmst du nicht erst die Schnittpunkte von Gerade und Kreis?

Answer 1

Ich komme bei der Kreisgleichung auf 

(x + 5)^2 + (y + 1)^2 = 20

checkst du das mal?

Comments

K: x^2 + y^2 + 10·x + 2·y + 6 = 0

G: 3·x + y + 6 = 0 --> y = g(x) = - 3·x - 6

G in K

x^2 + (- 3·x - 6)^2 + 10·x + 2·(- 3·x - 6) + 6 = 0 --> x = -3 ∨ x = -1

Dazu die y-Koordinaten

g(-3) = 3  

g(-1) = - 3

Berechne den Winkel Zwischen der Geraden und dem Radius zum Schnittpunkt. Aber Achtung. Dieser Winkel unterscheidet sich um 90 Grad.

---

Danke,bin jz auch auf r=20 gekommen

S Punkte sind kein Problem!

Soll es aber mit dieser Formel berechnen!

Stimmt mein beliebiger Punkt mit (-3/3)?

Wenn ich einsetze in die Formel kommt

Betrag(-5/-1)-(-3/3).1/wurzel18.(-3/3)betrag

Das 2 (-3/3) entnehm ich doch dem 1 Schnittpunkt?

Komme da einfach nicht auf die L

---

Habs nun doch!

No erhalte ich ja aus g und ist somit (3/1), eingesetzt komm ich dann auf 45 grad

Danke

Answer 2

Dein Radius stimmt schon nicht

Answer 3

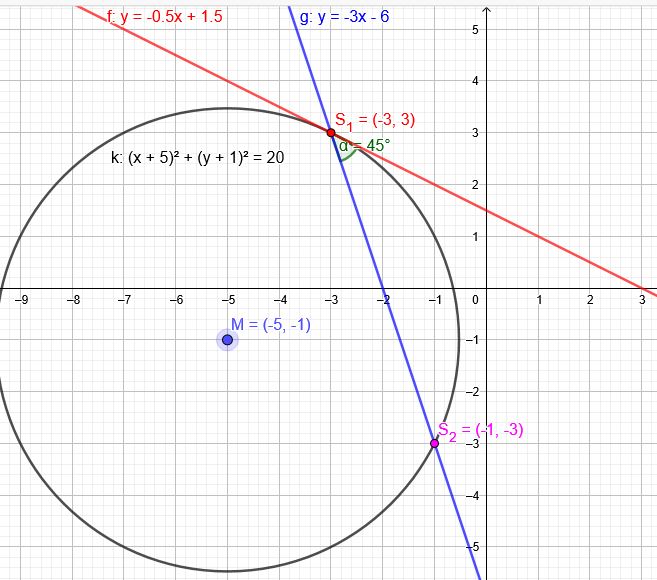
\(x^2+y^2+10x+2y+6=0\) g:  \(3x+y+6=0\)   →  \(y=-3x-6\) Schnitt mit Kreis

\(y=-3x-6\)

\(x^2+(-3x-6)^2+10x+2\cdot(-3x-6)+6=0\)

\(x_1=-3\)   \(y_1=3\)

Steigung der Tangente in  \(B_1(\red{-3}|\blue{3})\)

Implizites Differenzieren:

\(k(x,y)=x^2+y^2+10x+2y+6\)

\(k_x(x,y)=2x+10\)

\(k_y(x,y)=2y+2\)

\(k'(x)=- \frac{k_x(x,y)}{k_y(x,y)}=-\frac{x+5}{y+1} \)

\(k'(\red{-3})=-\frac{\red{-3}+5}{\blue{3}+1}=-\frac{1}{2} \)

Winkel zwischen Tangente und Gerade:

\(\tan(α)=| \frac{m_2-m_1}{1+m_1\cdot m_2}  |\)

\(m_2=-3\)    \(m_2=-\frac{1}{2}\)

\(\tan(α)=| \frac{-3+\frac{1}{2}}{1+(-3)\cdot (-\frac{1}{2}}) |=1\)

\( tan^{-1}(1)=45° \)

2.Tangente analog

Comments

2.Tangente analog

Das ist unklughaft.

Ersetze "analog" durch "überflüssig, weil ..."

---

Das ist unklughaft.

Finde ich nicht, weil FS dann den Weg selbst nochmal gehen müssen. So können sie dann feststellen, ob sie es verstanden haben.

---

weil FS dann den Weg selbst nochmal gehen müssen.

Nein, sie müssen die Gleichung der zweiten Tangente nicht ausrechnen. Sie müssen nicht einmal den zweiten Schnittpunkt kennen.

Und tu nicht so, als würdest du Beiträge schreiben, um Fragestellern zu helfen.

---

Wie soll das denn gehen?

Und tu nicht so, als würdest du Beiträge schreiben, um Fragestellern zu helfen.

Fang nicht an, gemein zu werden!

---

Wie soll das denn gehen?

Ich weiß auch nicht, wie es in deinem Fall gehen soll, dass deine Beiträge Fragestellern helfen. Aber das Thema ist ausreichend durchgekaut.

Was das konkrete fachliche Thema betrifft: Auch die zweite Tangente (die in S2) schneidet die Sekante mit dem gleichen Schnittwinkel wie die Tangente in S1 das tut.

---

Es ist hier weder die Ableiterei noch die Berechnung der Schnittpunkte notwendig.

Aus der Kreisgleichung folgt Mittelpunkt \(m\) und Radius \(r=\sqrt{20}\) des Kreises. Setze \(m\) in die normierte Geradengleichung ein und erhalte den Absolutwert \(d=\sqrt{10}\). Es ist$$\alpha = \arccos\left(\frac{d}{r}\right)=45\degree$$ genau so wie es der Fragesteller auch schon angesetzt hatte.

---

Es ist hier weder die Ableiterei noch die Berechnung der Schnittpunkte notwendig.

Aber es ist ein Weg, wenn die normierte Geradengleichung und die Winkelformel nicht bekannt sind.

---

Und wenn man sich schon die unnötige Mühe der Berechnung beider Schnittpunkte gemacht hat, ist der gesuchte Winkel die Differenz aus 90° und der Größe eines Basiswinkels (orange) im abgebildeten gleichschenkligen Dreieck.