Rechtecke unter Funktionen/ Extremwertprobleme

Question

Recktecke unter Funktionen
Aufgabe: Es wird ein Rechteck untersucht, bei dem zwei Seiten auf den Koordiantenachsen liegen und ein Eckpunkt auf dem Funktionsgraph von f(x) = -x + 6. Bestimme das Rechteck mit dem maximalen Flächeninhalt.

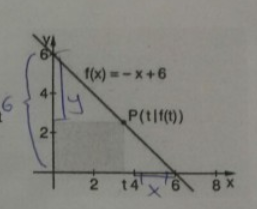
ich habe irgendwie Schwierigkeiten bei einer Mathe-Aufgabe und wollte wissen, ob ihr mir weiterhelfen könnt.

Einen Lösungsansatz hab ich aber ich weiß nicht recht, ob der richtig ist, weil das Ergebnis nicht sein kann.

f(x) = -x+6

f(x) = (6-x) * (6-(-x+6)

= (6-x) * (6+x-6)

= (6-x)* (x)

= 6x-x²

f ' (x) = 6 - x

0 = 6-x

x = 6

Aber das kann gar nicht sein ! Was habe ich falsch gemacht ? etwa etwas beim ausmultiplizieren?

Answer 1

Vorüberlegung:
Das Rechteck soll maximalen Flächeninhalt haben. Die Seitenlänge soll t bzw. f(t) sein. Aus der Grafik kann man ersehen, dass t zwischen 0 und 6 sein muss und f(t) auch. Das Produkt wird am größten, wenn die Werte t und f(t) nahe beieinander liegen. So kann man schon grob schätzen, dass t etwa bei 3 liegen muss.

Nachweis:
A = t * f(t) = t * (-t+6)
A = -t² +6t
A' = -2t+6 
0  = -2t +6
t   = 3 => f(t) =3 => A = 9