Bei der folgenden Aufgabe habe ich zwar schon die Lösungen aber ich frage mich trotzdem wie man darauf kommt!? Kann mir jemand plausible Rechenwege zeigen? (Lösung der Aufgabe siehe unten)
Aufgaben:
6.1 Gegeben ist die zweite Ableitung der Funktion \( f \) durch die Gleichung
\( \mathrm{f}^{\prime \prime}(\mathrm{x})=\frac{1}{2} \mathrm{x}-2 \quad \text { und } \quad \mathrm{D}_{\mathrm{f}}=\mathrm{R} \)
Bestimmen Sie rechnerisch die Gleichung der Funktion \( f \) so, dass die Gerade \( \mathrm{t} \) mit \( \mathrm{t}(\mathrm{x})=-\mathrm{x}+\frac{16}{3} \) Wendetangente des Graphen von \( \mathrm{fist} \).
6.2.0 Betrachtet wird im Folgenden die reelle Funktion f mit der Gleichung
\( \mathrm{f}(\mathrm{x})=\frac{1}{10} \mathrm{x}^{3}+\frac{1}{5} \mathrm{x}^{2}-\frac{3}{2} \mathrm{x} \quad \text { und } \quad \mathrm{D}_{f}=\mathrm{R} \)
Der Graph der Funktion f heißt \( \mathrm{G}_{\mathrm{f}} \).
6.2.1 Skizzieren Sie den Graphen \( \mathrm{G}_{\mathrm{f}} \) in ein geeignetes Koordinatensystem.
6.2.2 Weisen Sie nach, dass jede Stammfunktion \( F_{\mathrm{c}} \) der Funktion f bei \( \mathrm{x}=0 \) eine Extremstelle besitzt.
6.2.3 Ermitteln Sie den Inhalt der Fläche, die der Graph \( \mathrm{G}_{\mathrm{f}} \) und die Abszissenachse im Intervall \( [-1 ; 2] \) begrenzen.
6.3.0 Gegeben ist eine weitere reelle Funktion \( \mathrm{p} \) durch ihre Gleichung
\( \mathrm{p}(\mathrm{x})=\frac{1}{10} \mathrm{x}^{2}+\frac{1}{2} \mathrm{x} \quad \text { und } \quad \mathrm{D}_{\mathrm{p}}=\mathbf{R} \)
Der Graph der Funktion p heißt \( \mathrm{G}_{\mathrm{p}} \).
6.3.1 Skizzieren Sie den Graphen \( \mathrm{G}_{p} \) in das vorhandene Koordinatensystem.
6.3.2 Eine Gerade \( x=u \) mit \( u \in R \) teilt die vom Graphen \( G_{p} \) und der Abszissenachse im dritten Quadranten vollständig begrenzte Fläche. Ermitteln Sie zwei mögliche Werte für u so, dass eine dieser Teilflächen den Inhalt von \( 1,5 ~ \mathrm{FE} \) besitzt.
6.3.3 Die Graphen \( \mathrm{G}_{\mathrm{f}} \) und \( \mathrm{G}_{\mathrm{p}} \) schließen im ersten und vierten Quadranten eine Fläche vollständig ein. Bestimmen Sie den Inhalt dieser Fläche.
Lösungen:
6.1 Funktionsgleichung:
\( \begin{array}{lll} \mathrm{f}^{\prime \prime}(\mathrm{x})=\frac{1}{2} \mathrm{x}-2 & \Rightarrow \mathrm{f}^{\prime \prime}(\mathrm{x})=0 \quad \Rightarrow \quad \mathrm{x}=4 \\ \mathrm{t}(\mathrm{x})=-\mathrm{x}+\frac{16}{3} & \Rightarrow \mathrm{t}(4)=\frac{4}{3} \quad \Rightarrow \quad \mathrm{w}\left(4 ; \frac{4}{3}\right) \\ \mathrm{f}^{\prime}(\mathrm{x})=\frac{1}{4} \mathrm{x}^{2}-2 \mathrm{x}+\mathrm{c} & \\ \mathrm{f}(\mathrm{x})=\frac{1}{12} \mathrm{x}^{3}-\mathrm{x}^{2}+\mathrm{c} \mathrm{x}+\mathrm{d} \\ \mathrm{f}^{\prime}(4)=-1 \\ \mathrm{f}(4)=\frac{4}{3} \quad \Rightarrow \quad-4+\mathrm{c}=-1 \quad \Rightarrow \quad \mathrm{c}=3 \\ & \Rightarrow \quad \frac{4}{3}+\mathrm{d}=\frac{4}{3} \quad \Rightarrow \quad \mathrm{d}=0 \\ & \Rightarrow \quad \mathrm{f}(\mathrm{x})=\frac{1}{12} \mathrm{x}^{3}-\mathrm{x}^{2}+3 \mathrm{x} \end{array} \)
6.2.1 Skizze:
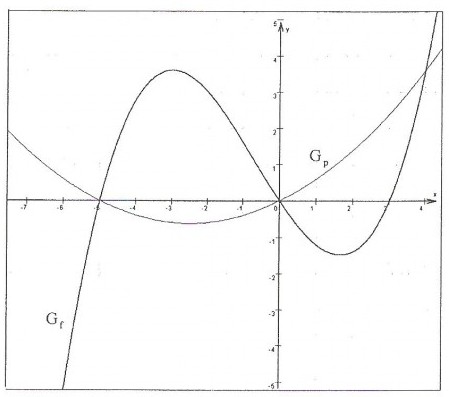
6.2.2 Nachweis der Extremstelle:
\( f(x)=\frac{1}{10} x^{3}+\frac{1}{5} x^{2}-\frac{3}{2} x \Rightarrow \quad F_{c}^{\prime}(0)=f(0)=0 \\ f^{\prime}(x)=\frac{3}{10} x^{2}+\frac{2}{5} x-\frac{3}{2} \Rightarrow \quad F_{c}^{\prime \prime}(0)=f^{\prime}(0)=-\frac{3}{2} \neq 0 \)
→ Jede Stammfunktion \( F_{c} \) besitzt eine Extremstelle bei \( x=0 \).
6.2.3 Flächeninhalt:
\( \begin{array}{l} {[\mathrm{A}]_{-1}^{2}=\left[\mathrm{A}_{1}\right]_{-1}^{0}+\left[\mathrm{A}_{2}\right]_{0}^{2}} \\ \begin{array}{l} \mathrm{A}=\int \limits_{-1}^{0} \mathrm{f}(\mathrm{x}) \mathrm{dx}+\left|\int \limits_{0}^{2} \mathrm{f}(\mathrm{x}) \mathrm{dx}\right| \quad \Rightarrow \quad \mathrm{A}_{1}=\frac{19}{24} ~ \mathrm{FE} \\ \mathrm{A}_{2}=\frac{31}{15} ~ \mathrm{FE} \\ \mathrm{A}=\frac{343}{120} ~ \mathrm{FE} \approx 2,86 ~ \mathrm{FE} \end{array} \end{array} \)
6.3.1 Skizze siehe unter 6.2.1
6.3.2 Werte für \( u \) :
\( \mathrm{A}=\left|\int \limits_{-5}^{u} \mathrm{p}(\mathrm{x}) \mathrm{dx}\right|=1,5 ~ \mathrm{FE} \quad \Rightarrow \quad \int \limits_{-5}^{u}\left(\frac{1}{10} \mathrm{x}^{2}+\frac{1}{2} \mathrm{x}\right) \mathrm{dx}=-1,5 \)
\( \left[\frac{1}{30} \mathrm{x}^{3}+\frac{1}{4} \mathrm{x}^{2}\right]_{-5}^{u}=-1,5 \quad \Rightarrow \quad \frac{1}{30} \mathrm{u}^{3}+\frac{1}{4} \mathrm{u}^{2}-\frac{7}{12}=0 \)
\( \Rightarrow \quad u_{1} \approx-7,16 \quad \) entfällt
\( \mathrm{u}_{2} \approx-1,74 \)
\( \mathrm{u}_{3} \approx 1,40 \quad \) entfällt
\( \mathrm{u} \approx-1,74 \)
wegen des Symmetrieverhaltens des Graphen \( \mathrm{G}_{\mathrm{p}} \) im Intervall \( [-5 ; 0] \) ergibt sich ein zweiter Wert für \( u \) wie folgt: \( -5-(-1,74)=-3,26 \)
\( u \approx-3,26 \)
ODER:
\( A=\left|\int \limits_{\mathrm{u}}^{0} \mathrm{p}(\mathrm{x}) \mathrm{dx}\right|=1,5 ~ \mathrm{FE} \quad \Rightarrow \quad \int \limits_{\mathrm{n}}^{0}\left(\frac{1}{10} \mathrm{x}^{2}+\frac{1}{2} \mathrm{x}\right) \mathrm{dx}=-1,5 \)
\( \left[\begin{array}{rl}\left.\frac{1}{30} \mathrm{x}^{3}+\frac{1}{4} \mathrm{x}^{2}\right]_{u}^{0}=-1,5 & \Rightarrow-\frac{1}{30} \mathrm{u}^{3}-\frac{1}{4} \mathrm{u}^{2}+\frac{3}{2}=0 \\ & \Rightarrow \quad \mathrm{u}_{1} \approx-6,40 \quad \text { entfällt } \\ & \mathrm{u}_{2} \approx-3,26 \\ & \mathrm{u}_{3} \approx 2,16 \quad \text { entfällt }\end{array}\right. \)
\( u \approx -3,26 \)
wegen des Symmetrieverhaltens des Graphen \( \mathrm{G}_{\mathrm{p}} \) im Intervall \( [-5 ; 0] \) ergibt sich ein zweiter Wert für \( u \) wie folgt: \( -5-(-3,26)=-1,74 \)
\( u \approx-1,74 \)
6.3.3 Fläche:
Schnittstellen bzw. Grenzen:
\( a=0 \qquad b=4 \)
\( \begin{array}{l} A=\int \limits_{0}^{4}(p(x)-f(x)) d x \\ A=\frac{112}{15} \mathrm{FE} \approx 7,47 ~ \mathrm{FE} \end{array} \)