Aufgabe:
Auf dem Dach des Hauses der Werbeagentur "Modern Art" wird das Werbelogo der Firma als dreieckiges Schild \( P_{1} P_{2} P_{3} \) montiert. Es gilt: \( 1 \mathrm{LE}=1 \mathrm{~m} \).
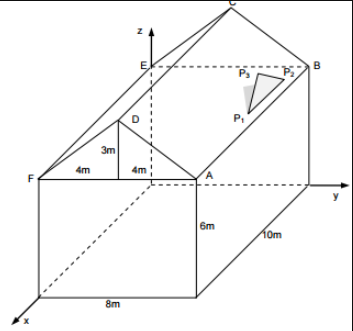
a) Der Punkt \( A(10|8| 6) \) ist ein Eckpunkt der rechten Dachfläche. Geben Sie die Koordinaten der anderen drei Eckpunkte \( B, C \) und \( D \) dieser Dachfläche an.
Bestimmen Sie eine Parametergleichung der Ebene, in der die Dachfläche \( A B C D \) liegt. Zeigen Sie, dass diese Ebene durch die Gleichung \( 3 y+4 z=48 \) beschrieben werden kann.
Berechnen Sie den Neigungswinkel dieser Dachfläche gegenüber der Ebene \( A B E F \).
b) Gegeben ist die Geradenschar \( g_{t}: \vec{x}=\left(\begin{array}{c}-3 \\ 6-4 t \\ 7,5+3 t\end{array}\right)+r\left(\begin{array}{c}-1 \\ 0 \\ 0\end{array}\right) r, t \in \mathbb{R} \).
Weisen Sie nach, dass die Geradenschar \( g_{t} \) die Ebene beschreibt, in der die rechte Dachfläche \( A B C D \) liegt.
Auf der Dachfläche wird ein Metallträger \( 30 \mathrm{~cm} \) äber der Ebene \( A B E F \) parallel zur Dachkante \( \overline{A B} \) angebracht. Die Lage des Metallträgers kann durch eine Gerade der Schar \( g_{t} \) beschrieben werden.
Berechnen Sie den Parameterwert \( t \).
Ansatz/Problem:
Mir geht es um b), der erste Satz "Weisen Sie nach, dass die Geradenschar g die Ebene beschreibt, in der die rechte Dachfläche ABCD liegt" Wie macht man das? Muss ich das wieder mit der Normalform nachweisen?