Extremwertbeispiele:
Beispiel 1: Aus einem rechteckigen Karton mit den Seiten \( 48 \mathrm{~cm} \) und \( 18 \mathrm{~cm} \) sind die Ecken so herauszuschneiden, dass der volumsgrößte offene Behälter gebildet werden kann.
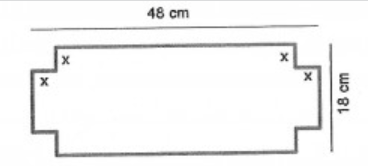
Beispiel 2: Aus drei Brettern der Breite \( a=1 \mathrm{~m} \) ist eine Rinne mit möglichst großem Querschnitt in Form eines gleichschenkligen Trapezes zu bilden.

Beispiel 3: Welches Rechteck vom gegebenen Umfang \( \mathrm{u}=8 \mathrm{~cm} \) hat die kleinste Diagonale d?
Beispiel 4: Handelsübliche Konservendosen haben angenähert eine zylindrische Form. Wie sind die Dosen mit einem Volumen von \( 500 \mathrm{ml} \) zu dimensionieren, wenn der Materialverbrauch bei der Herstellung minimal werden soll? Die Dicke des Blechs soll für Wand, Deckel und Boden gleich sein.

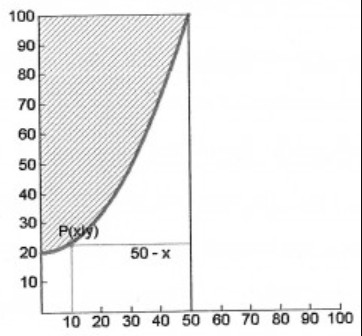
Beispiel 5: In der Fahrzeugindustrie werden aus rechteckigen Bleichstücken mit der Länge \( 100 \mathrm{~cm} \) und der Breite \( 50 \mathrm{~cm} \) die in der nebenstehenden Abbildung schattierten Flachenstücke herausgeschnitten.
Der Rand dieses Blechstückes kann in einem Koordinatensystem durch die Parabel mit \( \mathrm{y}=\frac{4}{125} \mathrm{x}^{2}+20 \) beschrieben werden.
Aus dem Reststück soll eine rechteckige Fläche F herausgeschnitten werden. Für welche Werte wird diese Fläche am größten?
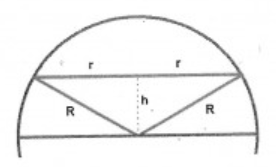
Beispiel 6: Einer Halbkugel (R) ist ein Drehkegel mit dem größten Volumen einzuschreiben, dessen Spitze im Kugelmittelpunkt liegt.
Beispiel 7: Eine Fensterfirma will ein neues Fenster auf den Markt bringen. Die Form soll ein Rechteck mit aufgesetztem Halbkreis sein. Wie sind die Abmessungen zu wählen, wenn der Umfang des Fensters \( 5 \mathrm{~m} \) betragen und mőglichst viel Licht eingelassen werden soll?
Beispiel 8: Dem von der Kurve \( y=4 x^{2} \) und der Geraden \( y=3 \) begrenzten Flächenstück ist ein gleichschenkeliges Dreieck von möglichst großem Flächeninhalt so einzuschreiben, dass seine Spitze im Punkt \( C(0 \mid 3) \) liegt.
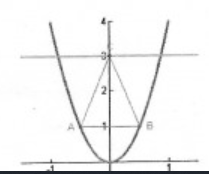
Ansatz/Problem:
Ich habe ein Problem bei Beispiel 6. Ich soll dabei einen Drehkegel im möglichst großem Volumen in eine Halbkugel legen. R soll ich wie eine reelle Zahl behandeln. Ich habe bereits einen Lösungsweg und ein Ergebnis, bin mir aber nicht sicher, ob mein Ansatz richtig ist. Da ich eine richtige Antwort brauche, wende ich mich an euch mit der Bitte mein Beispiel möglicherweise zu korrigieren.
