Stetig differenzierbar

Question

Hallo liebes Forum...

Ich hab ein Problem in Analysis und ich hoffe ihr könnt mir helfen.

Also gegeben ist die Funktion:

xe^-⟨x⟩   

Die Frage ist nun ob die Funktion stetig differenzierbar ist. Was Stetigkeit ist weiß ich nur ich tue ich mir schwer das nachzuweißen. Meine Idee wäre das über die Polstellen zu klären aber eigentlich kann einen Funktion trotz Polstellen stetig sein oder irre ich mich da?

Ich hoffe ihr könnt mir helfen...

Lg

Comments

f(x) = x·e^{-x}

Wisst ihr das x und e^x stetig sind ?

Dann könnte man argumentieren, die Verknüpfung (+, -, *) oder die Verkettung stetiger Funktionen ist wieder eine stetige Funktion.

---

soll das im Exponent ein Betrag sein, was soll sonst die seltsame Klammer?

---

Ja das sollen Betragsstriche sein. Sry kenn mich noch nicht so gut mit den Editor aus.

Nein es ist nicht gegeben das die f(x) stetig ist.

Konkred lautet die Fragestellung:

Ist die Funktion f(x)....auf ganz ℝ stetig differenzierbar(genaue Begründung)?

---

Betragsstriche sind die senkrechten Striche

f(x) = x * e^{-|x|}

Weißt du was es bedeutet wenn eine Funktion stetig ist? Weißt du wie man das erkennen kann bzw. wie man das mathematisch nachweisen kann?

Weißt du was es bedeutet wenn eine Funktion differenzierbar ist? Weißt du wie man das erkennen kann bzw. wie man das mathematisch nachweisen kann?

Ein Blick in dein Skript könnte hilfreich sein.

---

Was es bedeutet wenn eine Funktion stetig ist weiß ich schon nur wie man das mathematisch nachweißt eben nicht! In meinem Skript ist leider nur die Definition zu stetigkeit zu finden,was mir aber sehr helfen würde wäre ein ähnliches Beispiel wie das obere in dem mathematisch gezeigt wird ob eine Funktion stetig ist!

Answer 1

stetig differenzierbar heißt:

Die Funktion ist überall differenzierbar und die Ableitung ist überallstetig.

Also bildest du die Ableitung - für x ungleich 0 mit den gängigen Sätzen -

und für x=0 mit dem Differenzenquotient. Und dann prüfe, ob die

so bestimmte Ableitung überall stetig ist.

Answer 2

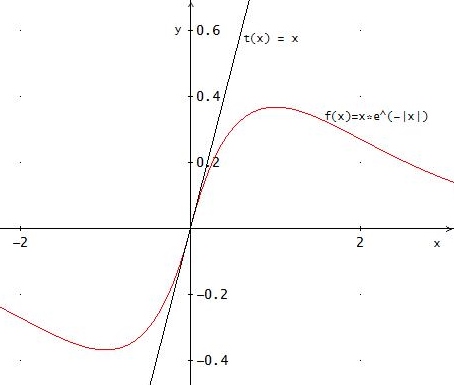
f(x) = x · e^{- |x|}

zuerst betragsfrei schreiben   [ |x| = x für x ≥ 0 und |x| = - x  für x<0 ]

f(x) = x · e^{- x}  für x ≥ 0

        x · e ^x   für x < 0

Für x ≠ 0 ist die eingeschränkte Funktion f_e als Komposition differenzierbarer Funktionen ebenfalls differenzierbar mit

 f_e '(x) = e^-x · (1 - x)   für  x>0

   e^x · (x+1)      f0r  x<0    [ ergibt sich aus der Produktregel [u•v] ' = u'•v + u•v' ]

An der Nahtstelle x=0 ist eine solche Funktion f genau dann differenzierbar, wenn

 f dort stetig ist und  lim_x→0+  f_e'(x)  = lim_x→0- f_e' (x) gilt:

f stetig in x= 0: 

  lim_x→0+  f (x) = 0 =   lim_x→0-  f (x)  = f(0)

 lim_x→0+  f_e'(x)  =  lim_x→0-  f_e'(x)  =  1

→  f ist in ℝ differenzierbar mit

f '(x) = e^-x · (1 - x)   für  x≥0

   e^x · (x+1)      f0r  x<0   

 lim_x→0+  f '(x)  =  lim_x→0-  f '(x)  =  1 = f '(0)

f ' ist deshalb stetig in x=0 und damit in ℝ. Aso ist  f in ℝ "stetig differenzierbar"

wünsche dir frohe Weihnachten

Gruß Wolfgang 

Comments

Wow, danke für die ausführlich Antwort!!! Danke das hilft mir denk ich weiter und ebenfalls Frohe Weihnachten. Danke nochmals