Quadratische Funktionen mit genau zwei, einem oder keinem Punkt auf der x-Achse. f(x) = x^2 - x + t

Question

Kann mir einer bitte erkären wie ich  die Aufgabe mit den Parameter lösen muss. Ich komm seit Stunden keinen Schritt weiter .

Answer 1

f(x) = x² - x + t

x^2 - x + t = 0
mit der quadratischen Ergänzung gelöst
x^2 - x + (1/2)^2 ) -t + (1/2)^2
( x - 1/2 )^2 = 1/4 - t  | Wurzelziehen
x -1/2 = ±√ ( 1/4 - t )
x = ±√ ( 1/4 - t ) - 1/2

Der Wert in der Wurzel muß positiv oder 0 sein
keine Lösung gibt es bei
1/4 - t < 0
t > 1/4

eine Lösung gibt es bei
1/4 - t = 0
t = 1/4

zwei Lösung gibt es bei
1/4 - t > 0
t < 1/4

Beispiele

t = 1/2 ( blau )
t = 1/4 ( rot )
t = -1/2 ( grün )

~plot~  x² - x + 1/2 ; x² - x + 1/4 ; x² - x -1/2 ~plot~

Comments

Könnten Sie mir vielleicht die 5d)  erklären komme da nicht weiter:)

---

Vorbemerkung : hier im Forum wird üblicherweise das " du " verwendet.

Hier eine Lösung durch Umformungen und quadratischer Ergänzung

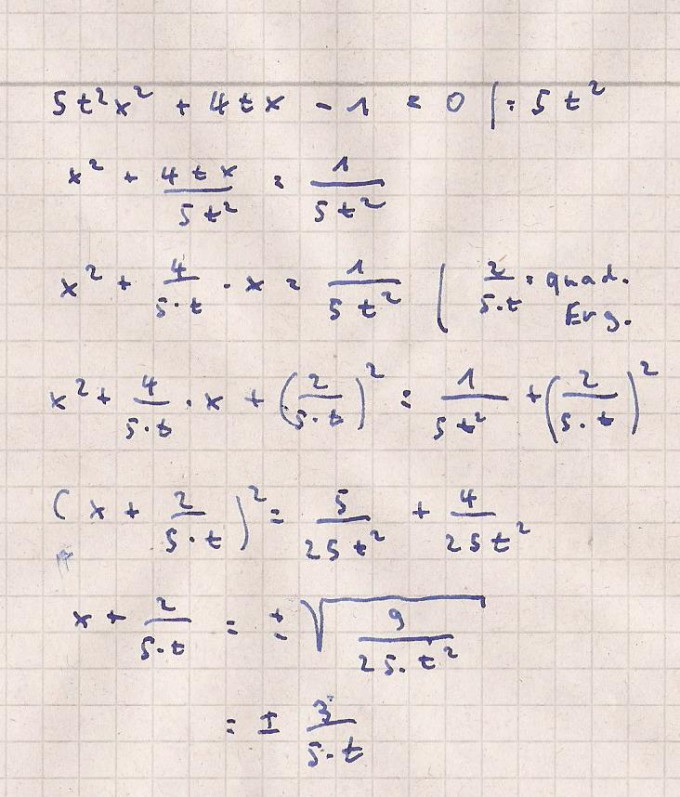
Die Frage ist nur ob es keine, eine oder 2 Nullstellen gibt.

Der Wurzelwert ist immer positiv da t im Quadrat vorkommt und damit auch immer
positiv ist.

Ausnahme t = 0 dann gibt es keine Lösung ( Division durch 0 ).

Für jedes t hat die Funktion 2 Nullstellen.

5 * t^2 *x^2 + 4 * t * x -1

blaue Kurve : t = 1
rote Kurve : t = -0.5

~plot~  5 * 1^2 *x^2 + 4 * 1 * x -1 ; 5 * (-0.5)^2 *x^2 + 4 * (-0.5) * x -1 ~plot~

Answer 2

du brauchst hier die Diskriminante (Stichwort in Wikipedia nachschauen) D = b^2 - 4ac 

f(x) = x^2 - x + t      , a=1, b= -1 , c = t

D = 1 - 4t

Für  D > 0 gibt es genau 2 Punkte auf der x-Achse

1 - 4t > 0

1 > 4t

1/4 > t.

Für  D = 0 gibt es genau 1 Punkt auf der x-Achse

1 - 4t = 0

1 =4t

1/4 =  t.

Für  D < 0 gibt es keinen Punkt auf der x-Achse

1 - 4t < 0

1 < 4t

1/4 < t.