Gleichung für einen Brückenbogen

Question

Folgende Frage kann ich nicht lösen:

Stahlbrücken haben eine ähnliche Form wie Steinbrücken - eine Parabel trägt mithilfe von senkrechten Stützen dei Brücke.Bei einer Stahlbrücke beträgt die Scheitelpunkthöhe der Parabel 45m. Die 4e Stütze ist von der Mitte der Parabel 50m entfernt und hat eine Höhe von 30m, die mittlere Stütze eine Höhe von 5m.

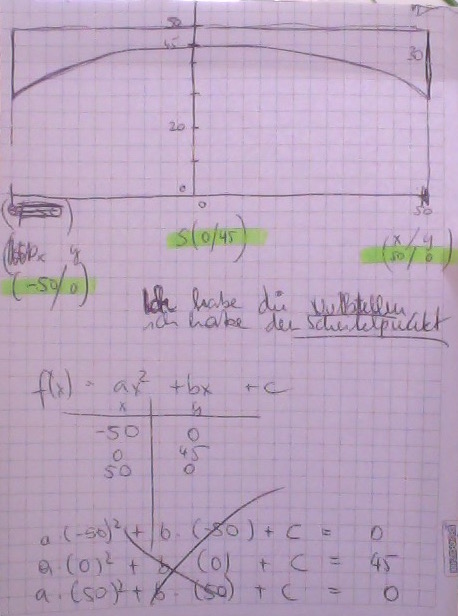
Fertigen Sie eine beschriftete Skizze an. Stellen Sie eine Funktionsgleichung b(x) auf, die diesen Brückenbogen beschreibt.

ok. die skizze habe ich geschafft.

Die Funktionsgleichung bereitet mir Sorgen.

Wie gehe ich an so etwas ran?

Ich habe 3 Punkte gegegeben (-50/0), Scheitelpunkt (45/0), (50/0). Wie gehe ich weiter? Die Matrix hat mich auch nicht auf das richtige Ergebenis gebracht. 

Answer 1

Ich würde mir die Parabel wie folgt vorstellen

Comments

"Der_Mathecoach": kannst du mir bitte deinen Lösungsweg aufschreiben?

ich weiß nicht genau wie ich an sowas rangehe.

Vor allem was und wie ich es in der Matrix eingebe.

Bzw: "mathef" hat mir die matrixpunkte angegeben.

Also ist die Matrix  

2500      -50       1         20  
0              0         1        45  
2500        50        1        20

ich versteh nicht, warum 2500 in der ersten Zeile positiv ist...

---

f(x) = a * x^2 + b

Du brauchst 2 Bedingungen. Die kannst du an der Skizze ablesen

f(0) = 45

a * 0^2 + b = 45 --> b = 45

f(50) = 20

a * 50^2 + 45 = 20 --> a = -0.01

Dann nur noch die Gleichung notieren

f(x) = - 0.01 * x^2 + 45

Dann noch ein Funktionsplotter nehmen und aus die Maus.

---

woher weiß ich dass ich hier nur 2 Bedigungen brauche?

---

nochmal:

2500      -50       1         20   

0              0         1        45   

2500        50        1        20

ich versteh nicht, warum 2500 in der ersten Zeile positiv ist...

---

woher weiß ich dass ich hier nur 2 Bedigungen brauche?

Erinnere dich an die Scheitelpunktform der Parabelgleichung.
y = a(x-d)^2 + b     mit Scheitelpunkt S(d|b).
Der Scheitelpunk hat gemäss Skizze d=0.
Daher ist der Ansatz
y = a(x)^2 + b 

zu empfehlen. 

---

Subtrahiere in deinem Ansatz die 1. Zeile von der letzten Zeile.

Dann hast du zuunterst

0   -100 0   0

und das sagt dir, dass (-100)*b = 0

Daher b= 0.

Answer 2

Die Parabel ist ja wohl sym. zur y-Achse, also Gleichung

 y= a*x^2 + b  Das b ist 45 und

dann

0 = a*50^2 + 45

- 45 = 2500*a

-0,018 = a

also    y = - 0,018 x^2 + 45

Comments

Geht aber mit deinem Ansatz auch.

Du siehst ja in der zweiten Zeile sofort  c=45.

Das eingesetzt gibt für die anderen beiden Variablen

die Matrix

2500  -50   -45
2500   50   -45

mit den Lösungen a=-0,018  und b = 0 .

---

Kannst du mir bitte genau aufschreiben was ich in die Matrix (3x4) eingeben muss! Danke.

---

Oder ist es nur eine 2x4 Matrix?

---

oder gar nur eine 2x3 matrix :)

---

Du musst die 50^2 und die (-50)^2 natürlich ausrechnen,

dann hast du

2500      -50       1         0
0              0         1        45
2500        50        1        0

---

Als 3x4 Matrix passt es zu dem Gl.system,
das du aufgeschrieben hattest.

---

Das Ergebnis lautet: b(x) = -1/100x^2 +45.
Da stimmen die Ergebnisse nicht überein .. ? ! ?

---

Du hattest ja ganz falsche Punkte.

Aus dem Text lese ich eher das ab:

(0;45) ;  (50;20)  denn wenn die Stütze 30m lang ist

und die Strasse ist ion der Höhe von 50, dann ist der

Parabelpunkt bei 20 und der linke bei

 - 50 / 20

Also ist die Matrix

2500      -50       1         20
0              0         1        45
2500        50        1        20

Dann passt es.

---

wie weiß ich, in welcher Reihenfolge ich die Punkte eingeben muss?

Ich hätte das ganze nämlich so eingegebn: 

0              0         1        45 
2500        50        1        20

2500      -50       1         20 

 

---

Also ist die Matrix 

2500      -50       1         20 
0              0         1        45 
2500        50        1        20

frage dazu: stimmt das positive 2500 in der ersten reihe oder sollte dies nicht auch -2500 sein?

---

Reihenfolge der Zeilen ist egal

-50 * - 50 = + 2500

Das + stimmt also.