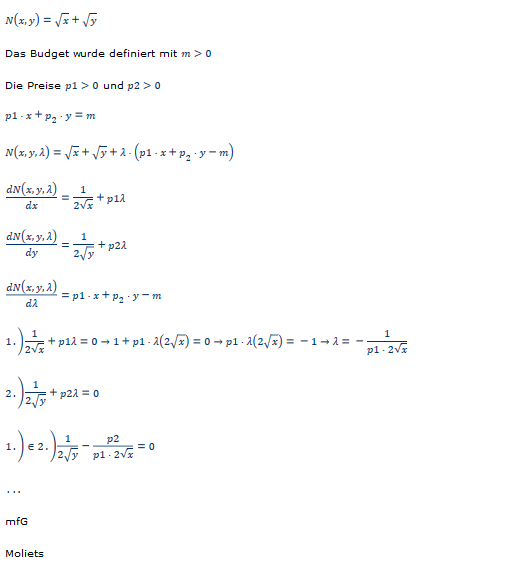
Text erkannt:
\( N(x, y)=\sqrt{x}+\sqrt{y} \)
Das Budget wurde definiert mit \( m>0 \)
Die Preise \( p 1>0 \) und \( p 2>0 \)
\( p 1 \cdot x+p_{2}-y=m \)
\( N(x, y, \lambda)=\sqrt{x}+\sqrt{y}+\lambda \cdot\left(p 1 \cdot x+p_{2} \cdot y-m\right) \)
\( \frac{d N(x, y, \lambda)}{d x}=\frac{1}{2 \sqrt{x}}+p 1 \lambda \)
\( \frac{d N(x, y, \lambda)}{d y}=\frac{1}{2 \sqrt{y}}+p 2 \lambda \)
\( \frac{d N(x, y, \lambda)}{d \lambda}=p 1 \cdot x+p_{2} \cdot y-m \)
1. \( ) \frac{1}{2 \sqrt{x}}+p 1 \lambda=0 \rightarrow 1+p 1 \cdot \lambda(2 \sqrt{x})=0 \rightarrow p 1 \cdot \lambda(2 \sqrt{x})=-1 \rightarrow \lambda=-\frac{1}{p 1 \cdot 2 \sqrt{x}} \)
2. \( ) \frac{1}{2 \sqrt{y}}+p 2 \lambda=0 \)
1. \( ) \in 2 \cdot \int \frac{1}{2 \sqrt{y}}-\frac{p 2}{p 1 \cdot 2 \sqrt{x}}=0 \)
4
mfG
Moliets