Warum reicht die Information, dass ein Teildreieck gleichseitig ist, um den Flächeninhalt zu bestimmen?
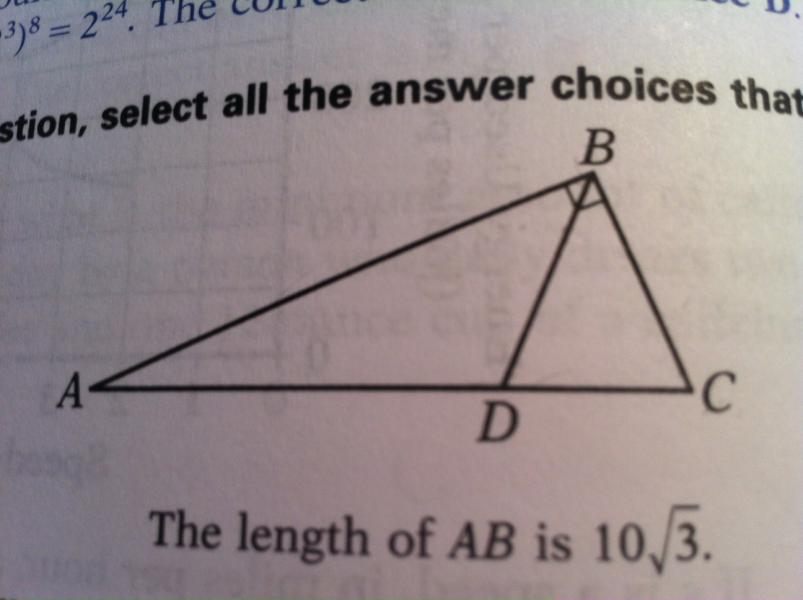
Im Buch stehen verschiedene Aussagen, wo man je überprüfen soll, ob sie allein ausreichen damit den flächeninhalt von ABC bestimmen kann.
Bei der folgenden Aussage verstehe ich aber nicht, warum sie ausreicht um den besagten flächeninhalt zu berechnen:
1) DBC ist ein gleichseitiges Dreieck.
Klar ist mir, dass dann der Winkel bei C 60 ist und der Winkel bei B ist in bezug auf das Dreick ABC ja eh 90, dementsprechend, ist der Winkel bei A 30. Aber warum kann man dann mit den gebenen Infos die Seite BC berechnen? (Um dann mit 1/2 * AB * BC den Flächeninhalt zu berechnen?)
!