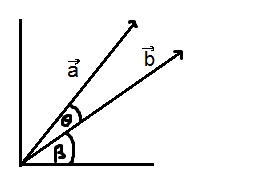
Ich habe die Winkel Θ und β wie unten im Bild dargestellt.Winkel zwischen
b und x-Achse ist β und Winkel zwischen
a und
b ist Θ
Ich soll nun für cos(α-β) und sin(α-β) die Größen cos Θ und sin Θ berechnen.
Meine Frage: mache ich das mit den Summenformeln? und woher kommt plötzlich α und wie mache ich das, wenn ich von den Vektoren keine Zahlen gegeben habe.
Ich weiß nicht wie ich ansetzen soll..