Gegeben ist ein Kreis mit dem Mittelpunkt im Punkt (2,1) und dem Radius 10.

Question

Gegeben ist ein Kreis mit dem Mittelpunkt im Punkt ( 2,1) und dem Radius 5.

Berechnen Sie die Nullstelle der Tangente, die den Kreis im Punkt (5 , 5) berührt?

Ich habe herausbekommen das die Steigung der Geraden durch Punkt (2,1) und (5,5) geht

d.h m= 4/3

brauche noch (Steigung der Tangente) , die Nullstellen und die Tangente

mir Erklärung bitte wenn es geht :)

Answer 1

Es gibt mehr als einen Weg zur Lösung. Einer davon ist der Weg über die Normalform einer Geraden: $\vec{n}\cdot\vec{x}=d$. Da sich $\vec{n}$ aus der Differenz des Berührpunktes B und dem Mittelpunkt M ergibt. Es ist $$\vec{n}=\vec{B}-\vec{M}=\begin{pmatrix}5 \\ 5 \end{pmatrix} - \begin{pmatrix}2 \\ 1 \end{pmatrix}=\begin{pmatrix}3 \\ 4 \end{pmatrix}$$ und d ist gleich $$d=\vec{n}\cdot\vec{B}=\begin{pmatrix}3 \\ 4 \end{pmatrix} \cdot \begin{pmatrix}5 \\ 5 \end{pmatrix}=35$$ Die Geradengleichung der Tangente t ist dann $$t: \quad \begin{pmatrix}3 \\ 4 \end{pmatrix} \cdot \vec{x}=35$$ Die Nullstelle erhält man indem man für $\vec{x}$ den Y-Wert auf 0 setzt. Also $$\begin{pmatrix}3 \\ 4 \end{pmatrix} \cdot\begin{pmatrix}x_0 \\ 0 \end{pmatrix}=35$$ daraus folgt die Nullstelle $$x_0=\frac{35}{3}$$ um die Steigung zu bestimmen schreibe ich die Tangentengleichung etwas anders:$$3x+4y=35$$ und nach y aufgelöst $$y=\frac{-3}{4}x + \frac{35}{4}$$Die Steigung m ist demzufolge $m=\frac{-3}{4}$.

Der zweite Weg geht über die Steigung. Mache Dir eine Zeichnung und Du siehst dass die Steigung der Tangente negativ ist und den Wert von $m=\frac{-3}{4}$ hat. Geht eine Gerade mit der Steigung m durch einen Punkt (u,v), so ist die Geradengleichung $y=m(x-u)+v$. Die Tangente t geht durch den Berührpunkt B (5,5) - also ist $$t: \quad y=\frac{-3}{4}(x-5)+5=\frac{-3}{4}x+\frac{15}{4}+5=\frac{-3}{4}x+\frac{35}{4}$$ die Nullstelle erhält man indem man y zu 0 setzt und x berechnet. das Ergebnis ist natürlich das selbe.

Gruß Werner

Answer 2

Hi,

Der Kreis ergibt sich zu:

(x-a)² + (y-b)² = r² mit M(a|b)

Bei uns also:

(x-2)² + (y-1)² = 5² = 25

Nun nach y auflösen:

y_(1,2) = 1 ± √(-x² + 4x + 21)

Wir wollen die Tangente in P(5|5) haben, deswegen nehmen wir den oberen Halbkreis (die beiden y-Funktionen beschreiben ja je eine Hälfte des Kreises). Den leiten wir nun ab:

y' = (2-x)/Wurzelterm

Nun setzen wir x = 5 ein -> y' = -0,75

Folglich lautet unsere Tangente t(x) = mx + b mit m = -0,75 und P(5|5)

5 = -0,75*5 + b

b = 8,75

--> t(x) = -0,75x + 8,75

Die Nullstelle ist demnach:

-0,75x + 8,75 = 0

x = 11 2/3

Zur Kontrolle:

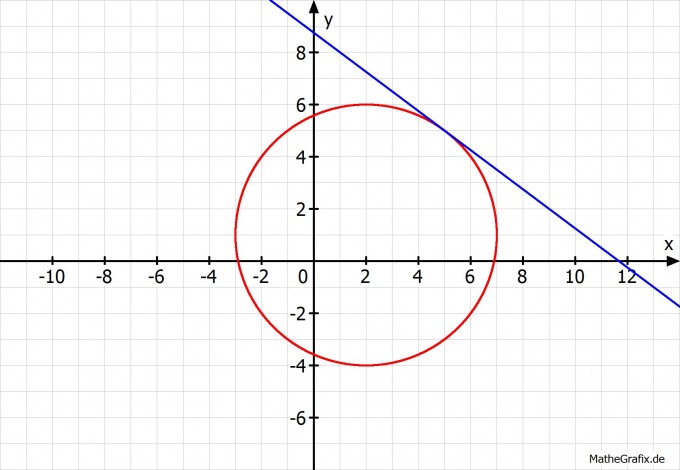
Grüße