Wenn Du beide Funktionen 'verketten' möchtest, so solltest Du sie zunächst jede für sich darstellen. Die Funktion \(\cos t\) beginnt für \(t=0\) bei 1 und ist die bekannte Schwingung (im Bild die gelbe Kurve). Die Steigung bei \(t=0\) ist 0 - also der Kurvenverlauf ist waagerecht. Die Nulldurchgänge liegen bei \(\pi/2\) und \(3\pi/2\) also etwa bei 1,6 und 4,7.
Die Funktion \(\frac{1}{e^t}=e^{-t}\) beginnt ebenso für \(t=0\) bei 1 und hat dort die Steigung -1 und nähert sich im weiteren Verlauf der X-Achse an (die orange Kurve).
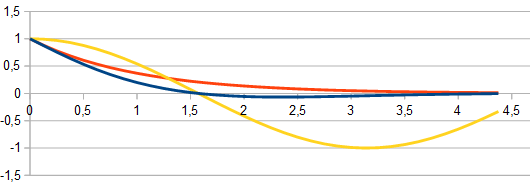
Durch die Multiplikation (Verkettung) beider Funktionen quetscht man sozusagen die Cosinus-Funktion mit der E-Funktion zusammen (blaue Kurve). Die E-Funktion begrenzt die Cosinus-Funktion sowohl nach oben, als auch nach unten. Nach unten, wenn man sich die E-Funktion an der X-Achse gespiegelt denkt. Die Anfangssteigung des Produkts ist jetzt die der E-Funktion - also -1. Das kann man sich leicht an Hand der Kettenregel der Ableitung klar machen. Da \(e\approx 3\) ist, hat das Produkt bei \(t=1\) nur noch etwas mehr als ein Drittel des Wertes von \(\cos(1)\), bei \(t=2\) ist es etwas mehr als ein 9'tel. Jenseits von \(t=3\) bleibt von der Schwingung nichts mehr übrig.
Die Multiplikation des Produkts mit \(1/2\) ändert nichts am grundsätzlichen Verlauf; es würde reichen bei der senkrechten Skala die 1 zu streichen und durch \(1/2\) zu ersetzen.
Dies ist übrigens der typische Verlauf einer gedämpften Schwingung.
Gruß Werner