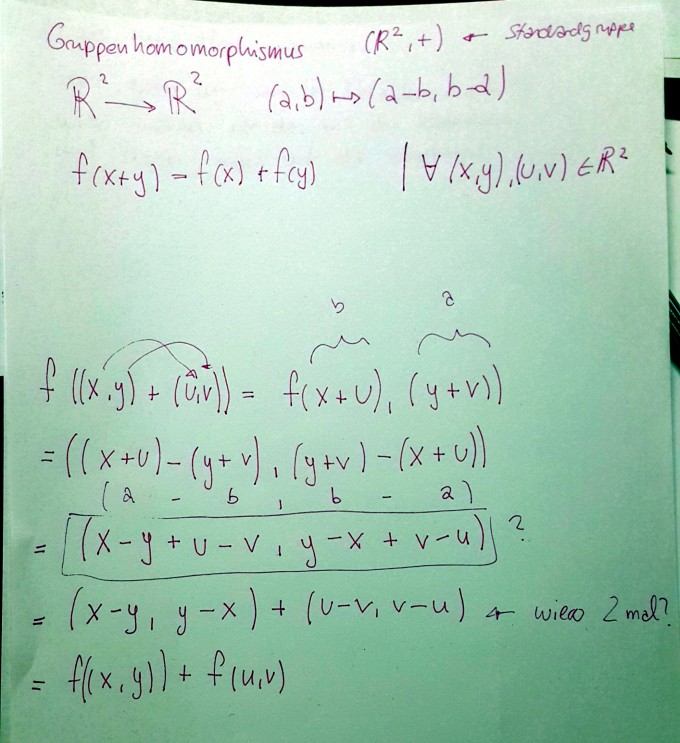Es geht um die Lösungen zur folgenden Aufgabe 2a (siehe Bild)
Ich verstehe die Umformung nicht ganz...
Wieso gehen wir von 4 Variablen aus? also, wieso nehmen wir nicht einfach nur 2? und auch die verdrehungen in der klammer verwirren mich. wieso nehmen wir x+u ? und wieso y+v ??
und vorallem die von mir in den Kasten gesetzte zeile verwirrt mich... kann mir vielleicht jemand so klar und kleinlich wie möglich erklären wie und WIESO diese umformungen zustande kommen ?
danke schonmal im Voraus
Aufgabenstellung ist ganz am ende.