Lösung der Aufgabe mit der imaginären Zahl

Question

Berechnen Sie: Im(2*e^{5*i})

Ich bitte um eine step-by-step-Anleitung

Answer 1

Im(2*e^5*i)


=  Im(2* ( cos(5) + i * sin(5)  )

=  Im(2* cos(5) + i * 2* sin(5)  )

=   2* sin(5) 

Comments

Leider kann ich die einzelnen Schritte nicht nachvollziehen, vorallem nicht wie Sie den Im bzw. i auflösen

---

Schau mal dort.

https://de.wikipedia.org/wiki/Komplexe_Zahl#Polarform

Und der Im-Teil ist immer der Term hinter dem i.

Answer 2

 
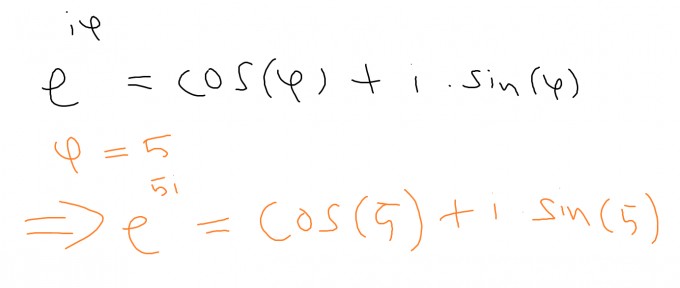
als erstes kannst Du mit der Formel $$e^{i\cdot\varphi}=cos(\varphi)+i\cdot\sin(\varphi)$$ mit $$\varphi=5$$ eine Umformung vornehmen und erhältst:  Nun musst Du lediglich die 2 mit der rechten Seite des orangen Terms multiplizieren. Der Imaginärteil ist der "Faktor bei dem i". Konnte ich Dir weiterhelfen?

André, savest8

Comments

Ja vielen Dank, jez hab ichs kapiert! :-)