für meine Abiturprüfung habe ich die alten Klausuren (hier Mathe LK 2014) durchgerechnet, verstehe aber leider den Rechenweg in dieser Lösung nicht.
Meine Aufgabe ist es, unter Verwendung von 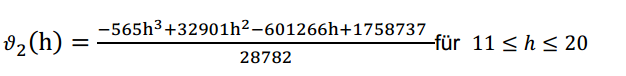 und
und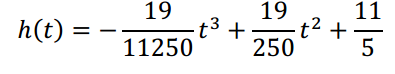
( h = Höhe, t = Zeit, ϑ = Temperatur) herauszufinden, nach welcher Zeit die niedrigste Temperatur gemessen wird.
Könnte mir jemand erklären wie man das macht?
Lösung:
