Symmetrie zur Y-Achse und Wendestellen g(x) = -1/2 a(e^{x/a} + e^{-x/a}) + 3a

Question

brauche mal ebene eure Hilfe bei einer Aufgabe.

In einem ersten Modell soll der gebogene Teil des Werkstückes durch eine Funktion g mit

$$g(x)=-\frac { 1 }{ 2 } a({ e }^{ \frac { x }{ a }  }+\quad { e }^{ -\frac { x }{ a }  })+3a$$ , x ∈ ℝ, a > 0 zwischen deren Nullstellen beschrieben werden.

Zeigen Sie allgemein:

Der Graph von g ist symmetrisch zur y-Achse.

g hat keine Wendestellen.

Bestimmen Sie die Gleichung der Funktion g so, dass die y-Achse bei 50 geschnitten wird.

Entscheiden Sie, ob das mit g für a = 25 modellierte Werkstück den folgenden Qualitätkriterien genügt:

Die Weite w des gebogenen Teils des Werkstückes soll kleiner als 90 cm sein.

Der Steigungswinkel des gebogenen Teils des Werkstücks soll im Punk P kleiner als 72° sein.

Ich habe nicht wirklich Ahnung was ich machen soll. Würde mich um Hilfe freuen.

EDIT:  g(x) = - 1/2 a(e^{x/a} + e^{-x/a}) + 3a  in der Fragestellung aus dem Minus ein Plus gemacht. Vgl. Kommentare zur Frage. 

Comments

Symmetrie zur y-Achse wird z.B. hier erklärt:

https://youtu.be/k3phlEIcd4Q

https://www.matheretter.de/wiki/achsensymmetrie

---

> Zeigen Sie allgemein:  Der Graph von g ist symmetrisch zur y-Achse.

f(-x) ≠ - f(x), denn in der Klammer dreht sich das Vorzeichen um, beim Summanden + 3a aber nicht.

Der Graph von g kann also nicht symmetrisch zur y-Achse sein.

Bevor man Lust hat, hier etwas zu rechnen, muss also erst einmal die Aufgabenstellung geklärt werden.

---

Hmmm, verstehe das immer noch nicht

---

 aber a is doch größer als 0, müsste es dann nicht im Prinzip auf das selbe hinaus laufen?

---

Die Graphen sind nicht symmetrisch zur y-Achse und sie haben jeweils einen Wendepunkt. In deiner Aufgabenstellung steht es anders. (wurde inzwischen editiert)

---

Ups, entschuldigung in der Klammer müsste eigentlich ein Plus stehen, würde es dann was ändern?

---

Das ändert alles!

 

---

Danke für die ganze Arbeit, aber ich bin gerade etwas durcheinander und verstehe gerade nicht wie ich nach a auflösen soll?

Answer 1

Hallo Bacardi,

nachdem Lu das mit der Symmetrie und den Wendestellen geklärt hat, bleiben noch einige Fragen offen:

>  Bestimmen Sie die Gleichung der Funktion g so, dass die y-Achse bei 50 geschnitten wird.

Schnittpunkt auf der y-Achse: x = 0

- 1/2·a·(e^0/a + e^{- 0/a} ) + 3·a = 50   ⇔  - 1/2·a · 2 + 3a = 50   ⇔  2a = 50 ⇔  a = 25 

             g(x) = -25/2 * ( e^x/25 + e^-x/25 ) + 75 

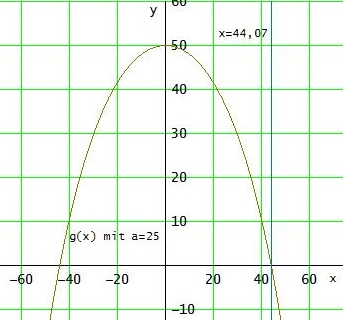
> Entscheiden Sie, ob das mit g für a = 25 modellierte Werkstück den folgenden Qualitätkriterien genügt:

> Die Weite w des gebogenen Teils des Werkstückes soll kleiner als 90 cm sein.

- 25/2 ·( e^x/25 +  e^-x/25 ) + 75 = 0    | * (-2/25)

 e^x/25 +  e^-x/25 - 6 = 0 

setze  z =  e^x/25

z + 1/z - 6 = 0        | * z

z² + 1 - 6z = 0

z² - 6z + 1 = 0

pq-Formel:

 z₁ ≈ 5.828427124  ;   z₂ ≈ 0.1715728752  

x₁ = 25 * ln(z) ≈ 44,07   ;  x₂  ≈ - 44,07   →  w  =  x₁ + x₂  ≈  89,14

Die Weite w ( = Abstand der beiden Nullstellen ) ist also kleiner als 90 cm.

> Der Steigungswinkel des gebogenen Teils des Werkstücks soll im Punk P kleiner als 72° sein.

Da kein Punkt P gegeben ist, soll man wohl den größten Steigungswinkel an der Nullstelle x₁ nehmen:

g' (x) = 1/2 * ( e^-x/25 -  e^x/25 )   →  mit x = Nullstelle x₁    g' (x₁) = -2.828427124

tan(α) = | -2.828427124 |   →   "Steigungswinkel" ≈ 70,53° < 72°    

( Ich denke, dass "..." mit dem Steigungswinkel gemeint ist. Eigentlich ist der Steigungswinkel der Winkel der Tangente mit der positiven Richtung der x-Achse, hier also 180° - 70,53° = 109,47° , was aber im Sinne der Qualitätskontrolle keinen Sinn machen würde. )

Gruß Wolfgang

Answer 2

g(x) = -1/2 a(e^{x/a} + e^{-x/a}) + 3a 

g(-x) = -1/2 a(e^{-x/a} + e^{-(-x)/a}) + 3a 

g(-x) = -1/2 a(e^{-x/a} + e^{x/a}) + 3a 

g(-x) = -1/2 a(e^{x/a} + e^{-x/a}) + 3a 

= g(x)

q.e.d Symmetrie zur y-Achse. Erklärung vgl. oben im 1. Kommentar verlinktes Video.

Kontrolle: Graph mit a=1 und a=2:

~plot~ [[-3|3|-1|12]]; -1/2 * (e^{x} + e^{-x}) + 3 ; -1/2 *2(e^{x/2} + e^{-x/2}) + 3*2 ~plot~

Comments

Sorry, dass ich immer frage aber ich verstehe das Video nicht. Wie soll ich nach -x auflösen, wenn a noch da ist?

---

Du musst nicht nach -x auflösen. Das Einzige, was du tun musst, ist überall, wo x steht einfach (-x) hinschreiben und dann umformen bis wieder g(x) dasteht.

---

Allfällige Wendepunkte findest du, wenn du die 2. Ableitung = 0 setzt.

Kontrolle der Ableitungen kannst du von https://www.wolframalpha.com/input/?i=f(x)+%3D+-1%2F2+e%5E(-x%2Fa)+(-1+%2B+e%5E((2+x)%2Fa)) haben:

Erste Ableitung

eingesetzt in Wolframalpha, berechnet dann die 2. Ableitung von g(x):

 

---

Ich glaube, dass ich langsam anfange es zu verstehen, aber wo hast du f1 in dem Diagramm her und inwiefern würde es ein Unterschied geben?

---

@geoborn: Die Tex-Formel mit dem Minus war vorgegeben. Da war ausserdem noch ein Minus in der Klammer. Vgl. Kommentar oben.

---

aber wo hast du f1 in dem Diagramm her und inwiefern würde es ein Unterschied geben?

Ich habe für a den Wert 1 eingesetzt -> f1 und dann a=2. Ich kann ja nicht für alle a gleichzeitig zeichnen. Du kannst selbst beliebige andere Werte für a nehmen für deine Zeichnung. Rechnen musst du aber nur das, was ich zu Beginn gerechnet habe. 

Answer 3

 g ( x ) = minus 1/2 * a * ( e ^{x/a} + e ^{-x/a} ) + 3a

g ( 0 ) = - 1/2 * a * ( e ^{0/a} + e ^{-0/a} ) + 3a = 50
g ( 0 ) = - 1/2 * a * ( e ^0 + e ^{-0} ) + 3a = 50
g ( 0 ) = - 1/2 * a * ( 1 + 1 ) + 3a = 50
g ( 0 ) = - 1* a  + 3a = 50
2 * a = 50
a = 25

Gezeigt :

Der Graph von g ist symmetrisch zur y-Achse.

g hat keine Wendestellen.

Bestimmen Sie die Gleichung der Funktion g so, dass die y-Achse bei 50 geschnitten wird.

Entscheiden Sie, ob das mit g für a = 25 modellierte Werkstück
den folgnden Qualitätkriterien genügt:

Unverständlich

Die Weite w des gebogenen Teils des Werkstückes soll
kleiner als 90 cm sein.

Der Steigungswinkel des gebogenen Teils des Werkstücks soll im Punk P kleiner als 72° sein.

mfg Georg

Comments

Die Weite w des gebogenen Teils des Werkstückes soll
kleiner als 90 cm sein.

Wenn man die y-Achse bis 0 zeichnet sieht man
das -45 < x  < 45 ist
Weite < 90
Sollte man auch noch rechnerisch nachweisen.

---

georgborn hat berechnet:  "Bestimmen Sie die Gleichung der Funktion g so, dass die y-Achse bei 50 geschnitten wird. " gerechnet. 

---

Der Steigungswinkel des gebogenen Teils des Werkstücks soll im Punk P kleiner als 72° sein.

g ( x ) = - 1/2 * a * ( e ^x/a + e ^-x/a ) + 3a

g ´ ( x ) = tan ( 72 ° )

Soviel zunächst