Dass die Scheinlösung nach der Probe nicht 0 ergibt, ist ja leicht herauszubekommen, ABER wie sieht es mit komplexen Zahlen aus, denn diese füllen oft die "Lücken" {für Wurzelfunktion sqrt(z) kein Problem; z=x + y*i ; Betragsfunktion deshalb, um keine 2 Diagramme für Real- & Imaginärteil getrennt betrachten zu müssen }:
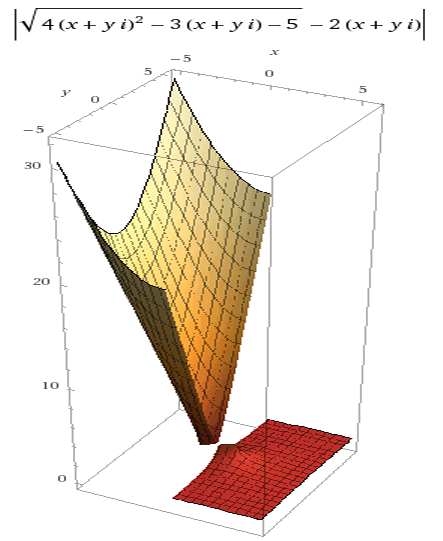
Auch mit komplexen Zahlen wird f(z)=0 (also der Boden der 3D-Grafik ) nicht erreicht.
Dann Versuche mit Grenzwert:
lim abs( + sqrt( 4 z^2 -5 - 3 z)-2 z),z->∞ ergibt 3/4
(ohne abs natürlich -3/4 )
und negativer Grenzwert ∞
Grenzwert um 0:
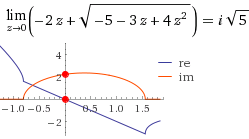
wird der Imaginärteil nicht 0 ...
-> also auch hier keine Möglichkeit, f(z) zu 0 zu bekommen.