Ich habe die Aufgabe in der ich mit zwei Punktein in der Ebene arbeite. Ich bin sehr unsicher weil ich immernoch in der Analysis denke und nicht vertraut bin mit Vektorenrechnung, Schreibweise, Begriffen.
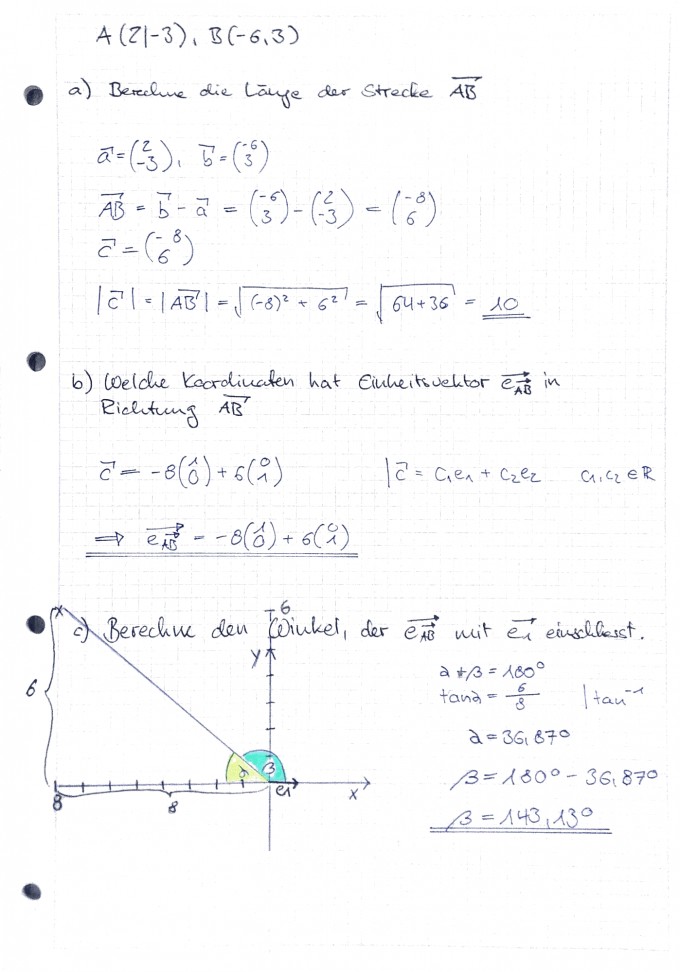
A( 2 I -3 ) und B( -6 I 3)
Aufgabe 1 - Länge AB berechnen
Aufgabe 2 - Koordinaten vom Einheitsvektor AB
Hier bin ich mir extrem unsicher, hier sollte ich doch den Vektor in e_(1) und e_(2) "zerlegen" und per Linearkombination meinen vektor c ausdrücken
Vektor c = c_(1)*e_(1) + c_(2)*e_(2) wobei e_(1) der Basisvektor mit der Länge eins ist und auf der X-Achse liegt, und e_(2) der Basisvektor auf der y-Achse ist und auch die Länge 1 beträgt. c_(1) und c_(2) ∈ ℝ
Aufgabe 3 - Winkel zwischen Einheitsvektor in Richtung AB und e_(1)
Ich ging davon aus das der Einheitsvektor in Richtung AB nichts anderes ist als c aber irgendwie hab ich den vom Ursprung aus gezeichnet obwohl mein Vektor c ein Verbindungsvektor zwischen A und B ist. So hab ich den Punkt oben links ober dem titel der Aufgabe c bekommen. e_(1) ist der Vektor auf der x-Achse mit der Länge 1.
Deswegen hab ich zuerst alpha berechnet weil ich betta nicht sofort ausrchnen konnte, da kein rechtwinkliges Dreieck gegeben ist.