Der Winkel 65° ist ein Peripheriewinkel gegenüber der Strecke \(AB\) wie folgende Skizze zeigt.
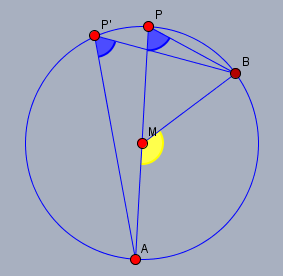
Der blaue Winkel \(APB\) bei \(P\) hat immer den Wert 65° egal wo sich der Punkt \(P\) auf dem Kreisbogen befindet. Zur Veranschaulichung habe ich Dir die Position \(P\prime\) eingezeichnet. Der gelbe Winkel ist der zugehörige Mittelpunktswinkel \(AMB\) und hat demnach den doppelten Wert - also 130°.
Und das gilt unabhängig von der Lage der Punkte \(A\) und \(B\) auf dem Kreis.
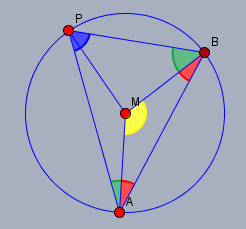
Da die Dreieck \(BPM\) und \(PAM\) gleichschenklig sind, sind ihre Basiswinkel gleich groß und folglich ist die Summe der grünen Winkel gleich dem blauen Winkel - dieser sei \(\varphi\). Die Winkelsumme im Dreieck \(ABP\) ist 180° folglich ist die Summe der roten \(=180°-2\cdot \varphi\). Und der gelbe Mittelpunktswinkel ist auf Grund der Winkelsumme im Dreieck \(ABM\) \(=180°- \sum{ rot}=180°-180°+2\varphi=2\varphi\).
Gruß Werner