Zeigen dass Matrix nicht nilpotent ist

Question

Sei die Matrix A:

      0 1 0

A = 0 0 0

      1 0 1

Für n >= 2 besteht A^n aus drei gleichen Vektoren v1, v2, v3 = (0 0 1)^t

Wie kann man damit zeigen, dass es keinen Nilpotenzgrad gibt, die Matrix also nicht nilpotent ist?

Comments

Man hat den Eindruck, Du weisst gar nicht, was es bedeutet: eine Matrix ist (nicht) nilpotent. Sonst wuerdest Du nicht die Lösung zur Aufgabe hinschreiben und dann noch fragen, wie die Lösung denn nun geht.

Answer 1

NC,

zum Anfang solltest Du Dir klar machen, was eine nilpotente Matrix ist:

Wir beginnen unsere Überlegungen damit zu prüfen, was passiert, wenn wir A mit sich selbst multiplizieren.

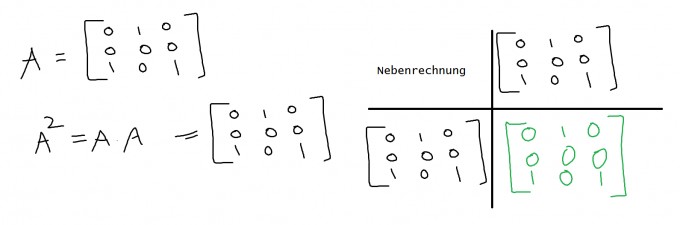
Wir sehen also, dass jede weitere Multiplikation von A wieder A als Ergebnis hat.

Egal wie oft wir A mit sich selbst multiplizieren: es wird niemals die Nullmatrix herauskommen! Mathematisch:

$$\not\exists n\in\mathbb{N}:A^n=N\text{ mit }N=0\in\mathbb{R}^{3\times3}$$

Daraus folgt direkt: A ist nicht nilpotent.

André

Answer 2

Hallo NC,

A² = A      (nachrechnen!)

  →   mit jeder weiteren Multiplikation mit A ergibt sich A

→   Aⁿ = A   ≠ Nullmatrix  für alle n∈ℕ

→  A ist nicht nilpotent

Gruß Wolfgang