Kreisgleichung bestimmen. Kreis zwischen x+y=10, x-Achse und y-Achse einbeschrieben

Question

Aufgabe

Der kreis liegt im 1. Quadranten, berührt die x-Achse, berührt die y-Achse und berührt auch die Gerade g mit der Gleichung x+y = 10.
Berechnen Sie den Gemeinsamen Punkt von K und g.

1. Schritt

g: x +y = 10
g: y = -x +10

Ich habe diese Gerade in ein Koordinatensystem eingezeichnet, fallende Steigung m= -1, Achsenabschnitt 10

2. Schritt

Ich hab gesehen, dass die Gerade mit den Koordinatenachsen ein rechtwinkliges und gleichschenkliges Dreieck ABO bildet.

A ( 0 I 10 ) 
B ( 10 I 0 )
O ( 0 I 0 )

Aufgrund der Lage des Kreises, muss der Kreis die Gerade g: y = -x +10 in dessen Mitte berühren.

Darum gilt,

$$\overrightarrow { x } =\quad { \overrightarrow { r }  }_{ A }+\frac { 1 }{ 2 } \overrightarrow { AB } \\ \begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} 0 \\ 10 \end{pmatrix}+0.5\begin{pmatrix} 10- & 0 \\ 0- & 10 \end{pmatrix}\\ \begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} 0 \\ 10 \end{pmatrix}+0.5\begin{pmatrix} 10 \\ -10 \end{pmatrix}\\ \begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} 0 \\ 10 \end{pmatrix}+\begin{pmatrix} 5 \\ -5 \end{pmatrix}\\ \\ x=\quad 5;\quad y=5$$

Das heisst, der Kreis schneidet die Gerade g: im Punkt P(5I5)

Doch wie bekomme ich nun den Radius und den Mittelpunkt. 

Ich habe ja die Parameterform des Schnittpunktes, ich könnte von dort aus eine Normale konstruieren, aber wie gross müsste dann das t sein
- was genau dem Radius entsprechen würde - 
damit ich zum Mittelpunkt komme?


Kreisgleichung

K: (x-u)^{2} + (x-y)^{2} = R^{2}

Hier wüsste ich nicht direkt was ich einsetzen kann

~draw~ gerade(0|10 10|0);punkt(0|10 "A(0I10)");punkt(10|0 "B(10I0)");punkt(5|5 "P(5I5)");;gerade(0|10 10|0);kreis(2.9|2.9 2.9);zoom(15) ~draw~

 

Comments

Bemerkung:

Den Kreis der im Plotter zu sehen ist, habe ch natürlich schätzungsweise eingezeichnet. 

---

Ist folgende Überlegung ein Trugschluss ?


Ich kann sagen, dass der Kreis bei einer doppelten Dreiecksfläche den Mittelpunk P
mit den Koordinaten
u= 5; v= 5 hätte

Wenn ich den nun einsetze, 

K: (x-5)^{2} + (y-5)^2 = R^{2}

Wenn der Mittelpunkt bei diesem Hypothetischen Kreis K aus 5 und 5 besteht, muss der Radius R 5 sein.

R=5


K: (x-5)^{2} + (y-5)^2 = 5^{2}

K: (x-5)^{2} + (y-5)^2 = 25 I 

So mit wäre, bei dem um die Hälfte kleineren Kreis, der tatsächlich gesucht ist der Radius R = 5/2 = 2.5

Aber hier Fehlern mit dann immernoch die Koordinaten des Mittelpunktes.

---

Eigentlich nicht, die ganze Rechnung muss nicht in einer ganzen Zeile stehen. Wieso?

---

ja, mit dem Wollte ich sagen, dass der kleinere Kreis - der auch tatsächlich gesucht ist - um die Hälfte kleiener Sein muss. 

Aber das wird wohl nicht stimmen, aber stimmt der Wert
und die Überlegung zum Berührungspiunkt K und g = P (5 I 5) ? Oder lag ich da schon falsch?

---

Nein deine Rechnung in der Frage ist ok. Aber etwas umständlich. 

Deine Rechnung wurde bei mir in einer Zeile angezeigt am Schluss stand x=5 ; REST unter dem Banner. Inzwischen ist sie aber auf meinem Bildschirm korrekt zu sehen. - Vermultich wurde der TEX-Teil nicht korrekt oder zu langsam geladen. 

---

Man kann die Aufgabe auch elementargeometrisch lösen, wenn man sie so formuliert: Welchen Radius hat der Inkreis eines gleichschenklig-rechtwinkligen Dreiecks mit der Kathetenlänge 10?

Answer 1

Den Berührpunkt (5/5) hättest du auch elementargeometrisch bestimmen können. Die Kreisgleichung lautet in diesenm Falle (x-r)²+(y-r)²=r². Hier setzt du x=5 und y=5 ein. Dann kannst du r bestimmen.

Comments

K : (x-r)^{2} + (y-r)^{2} = r^{2} I x= 5; y= 5
K : (5-r)^{2} + (5-r)^{2} = r^{2} 

25 -10r + r^{2} + 25 - 10r + r^{2} = r^{2}
50 -20r + 2r^{2} = r^{2} 
r^{2} -20r +50 = 0

r_(1) = 2,9289321881345245
r_(2) = 17,071067811865476

Das sind mega komische Werte für r, was kann ich jetzt sagen, dass der Radius 2,9 beträgt oder 17,7 (eher unwahrscheinlich). 

Und das der Mittelpunkt M ( 2.9 I 2.9 ) ? Trifft gemäss Zeichnung (Plott) zu. 

---

r₁ = 2,9289321881345245 Dieser Wert ist zutreffend, genauer r=10-5·√2
r₂ = 17,071067811865476Dieser Wert muss verworfen werden.

---

Super, ja beim Einsetzen und Auflösen hatte ich auch 

r_(1) = 10 - 5* √(2) 
r_(2) = 10 + 5* √(2) 

Wieso weisst du dass r_(2) verworfen wird, weil es gemäss Zeichnung nich möglich sein kann, oder?

---

Hallo limonade, durch deine Frage angregt habe ich noch einmal nachgedacht. Der Kreis nit dem Radius r₂ = 10 + 5* √(2) existiert tatsächlich und berührt ebenfalls die Koordinatenachsen und die gegebene Gerade, letzere allerdings von "außen".

---

Genau, es gibt neben dem r_(1), der den Radius des Kreises innerhalb des Dreiecks ABO bezeichnet noch einen zweiten Kreis r_(2) der diese Bedingungen erfüllt.

Welche Bedingungen erfüllt der?

Er berührt die x-Achse in einem Punkt.

Er berührt die y-Achse in einem Punkt.

Er berührt die gerade g: y= -x +10 im Punkt P (5 I 5)

Ich werde dies mit dem Plotter konstruieren versuchen um es grafisch für mich zu verdeutlichen.

Aber ein grosses Dankeschön für die Hilfe und die nachvollziehbaren Erklärungen!

---

~draw~ gerade(0|10 10|0);punkt(0|10 "A(0I10)");punkt(10|0 "B(10I0)");punkt(5|5 "P(5I5)");;gerade(0|10 10|0);kreis(2.9|2.9 2.9);vektor(0|0 17.07|17.07 "a");;kreis(17.07|17.07 17.07);zoom(40) ~draw~

Answer 2

Aus Symmetriegründen muss der Berührungspunkt genau zwischen A und B liegen.

Also P( (0+10)/2 | (10 + 0)/2 ) = P(5|5)

A ( 0 I 10 )  
B ( 10 I 0 ) 
O ( 0 I 0 ) 

Comments

Deine Rechnung wurde bei mir in einer Zeile angezeigt am Schluss stand x=5 ; REST unter dem Banner. Inzwischen ist sie aber auf meinem Bildschirm korrekt zu sehen.

K: (x-5)² + (y-5)² = 5²  

Ist die Gleichung eines Kreises mit Mittelpunkt M(5|5) und Radius r=5. 

Weder Mittelpunkt noch Radius passen zum gesuchten Kreis. 

Ansatz für die Kreisgleichung ist aus Symmetriegründen M(u|u) 

K: (x-u)^2 + (y - u)^2 = r^2       

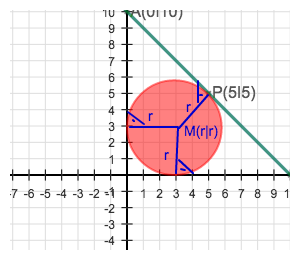
Ausserdem ist u = r. Da M(r|r) ist. 

Also

(x-r)^2 + (y-r)^2 = r^2 

P(5|5) liegt auf diesem Kreis.

(5-r)^2 + (5-r)^2 = r^2 

2(5-r)^2 = r^2   | √ und aus geometrischen Gründen kein - 

√(2)(5-r) = r 

5*√(2) - r*√(2) = r 

5*√(2) = r (√(2) + 1) 

(5 * √(2))/( √(2) + 1) = r 

Rechnung ohne Gewähr! 

---

"Aus Symmetriegründen" bedeutet, rechtwinkliges Dreieck, und gleichschenklig?

---

Richtig. Gleichschenklig und rechtwinklig.

Bitte. Gern geschehen!

---

Wenn du exakt hast:

"Der kreis liegt im 1. Quadranten, berührt die x-Achse, berührt die y-Achse und berührt auch die Gerade g mit der Gleichung x+y = 10. "

 könntest du den Kreis eigentlich auch weiter oben und rechts von x+y = 10 einzeichnen. Er ist dann nicht "eingeschlossen" berührt aber auch alle Geraden wie verlangt. 

Passt dann  aber diese Gleichung (5-r)² + (5-r)² = r²  noch zur ergänzten (gedachten) Skizze? 

Es ist immer noch M(u|u) und u = r.

Also ja. 

2(5-r)² = r²   |  Lasse einfach mal ein Minus zu. r ist dann grösser als 5 und 5-r kleiner als 0.

-√(2)*(5-r) = r

usw.

---

Vielen Dank Lu für deine auführlichen Erklärungen! 

Ich wusste nicht, dass ich die Koordinaten des Berührungspunktes in die Kreisgleichung für das x und y einsetzen darf und danach nach r auflöse

Weiter ist es ja logisch, dass neben dem Radius innerhalb des Dreiecks noch ein weiterer zweiter Radius existiert der die geforderten Bedingungen erfüllt, einfach ausserhalb und dementsprechend ist der Kreis und sein Radius r_(2) grösser als r_(1). 

Ich muss den allerdings nochmal mit dem Plotter konstruieren um es für mich grafisch zu verdeutlichen. 

Vielen, vielen Dank für die HIlfe !

---

~draw~ gerade(0|10 10|0);punkt(0|10 "A(0I10)");punkt(10|0 "B(10I0)");punkt(5|5 "P(5I5)");;gerade(0|10 10|0);kreis(2.9|2.9 2.9);vektor(0|0 17.07|17.07 "a");;kreis(17.07|17.07 17.07);zoom(40) ~draw~

---

Schön gemacht!