poission approximation / grenzwertsatz

Question

Ich habe noch etwas Schwierigkeiten mit der Poisson-Approximation. Wie muss ich hier vorgehen. Wir haben den Poissionschen Grenzwertsatz so definiert: (λ^k/k!)·e^-λ

Ich verstehe nicht was ich für λ einsetzen muss. 

Comments

Also das λ habe ich nun bestimmt als n ·p = 100 ·0,02 = 2

Für a) habe ich dann k =0 gesetzt und erhalte 13,5% als Ergebnis. Ist das so korrekt ?

Für b) habe ich mir das gegenereignis angeguckt also 1-P(kleiner gleich 1). Da komme ich auf 59%.

Bei c) stehe ich leider noch komplett auf dem schlauch

Answer 1

Lambda ist der Erwartungswert und gleichzeitig die Varianz der Poisson-Verteilung.

Comments

Also das λ habe ich nun bestimmt als n ·p = 100 ·0,02 = 2

Für a) habe ich dann k =0 gesetzt und erhalte 13,5% als Ergebnis. Ist das so korrekt ?

Für b) habe ich mir das gegenereignis angeguckt also 1-P(kleiner gleich 1). Da komme ich auf 59%.

Bei c) stehe ich leider noch komplett auf dem schlauch

---

(i) Auf 13,5 % bin ich auch gekommen (= e^-2).

Es wird aber nach exakter und approximierter Lösung gefragt.

 

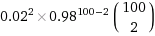
ist 27,3 %.

(ii) Das Vorgehen erscheint mir richtig, dein Resultat habe ich aber nicht nachgerechnet. Auch hier werden zwei Antworten verlangt.

(iii) Zähle die Wahrscheinlichkeiten zusammen für k=0, k=1, k=2 usw. bis du auf 50 % kommst. Und das wiederum für Binomial- und Poissonverteilung

---

Alles klar jetzt hab ichs! Danke :)