Ich versuche einen Algorithmus zu implementieren, der 2 Geraden mit einer Kurve verbindet.
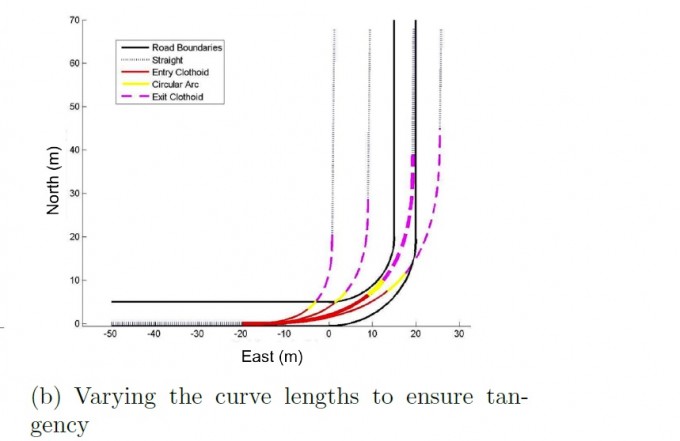
Die Kurven sind dabei in 3 Abschnitte unterteilt: Eingangsklothoide (Länge Lc1), Konstant-Radius-Bogen (Länge La) und Ausgangsklothoide (Länge Lc2)
Die Abschnitte kann man einzeln in Abhängigkeit des zurückgelegten Weges s ausdrücken (siehe Foto 2)..
für die innere Schleife des Algorithmus muss ich zuerst Lc1 raten und die anderen Abschnitte sind über feste Konstanten mit Lc1 berechenbar
( La= K1 * Lc1 , Lc2=K2 * Lc1)
Das Problem ist nun, dass ich prüfen muss, ob die entstandene Kurve tangential zur nächsten Gerade ist. Und wenn sie es nicht ist, muss mit dem Newton- Raphson- Verfahren ein neues Lc1 geschätzt werden. In meiner Quelle steht leider keine Formel dafür dabei.... wie mache ich das?