f(x) = x^3 - x^2 - x + 1
f'(x) = 3·x^2 - 2·x - 1
f''(x) = 6·x - 2
a) Berechne die Nullstellen, Hoch- und Tiefpunkte und den Wendepunkt des Graphen von f. Skizziere anschließend den Graphen im Intervall I = [-1,5; 2 ]
Nullstellen bei x =-1, x =1
Extrema Minimum ( 1 | 0 ), Maximum ( -1/3 | 1,1851 )
Wendepunkte Wendepunkt ( 1/3 | 16/27 )
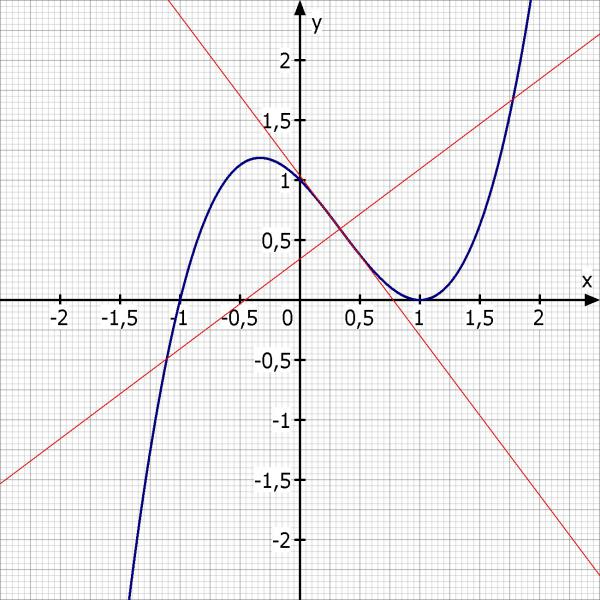
Skizze siehe unten.
b) Bestimme die Gleichung der Wendetangenten von f.
t(x) = f'(1/3) * (x - 1/3) + f(1/3) = -4/3 * (x - 1/3) + 16/27
c) Bestimme die Gleichung der Normalen n durch den Wendepunkt.
n(x) = f'(1/3) * (x - 1/3) + f(1/3) = 3/4 * (x - 1/3) + 16/27
d) Die Wendetangente und die Normale durch den Wendepunkt schließen mit der x-Achse eine Fläche ein. Trage diese Fläche in deine Skizze aus a) ein und berechne anschließend ihren Inhalt.
t(x) = 0
-4/3 * (x - 1/3) + 16/27 = 0
x = 7/9
n(x)=0
3/4 * (x - 1/3) + 16/27 = 0
x = - 37/81
A = 1/2 * (7/9 - (- 37/81)) * 16/27 = 800/2187 = 0.3657978966
e) Es wird nun die Funktion g mit g (x) = c * f (x) mit c > 0 betrachtet. Wie verändern sich die Lage des Wendepunktes und der Verlauf der Wendetangenten, wenn c wächst? Begründe.
Dei x-Koordinate des Wendepunktes ändert sich nicht. Die y-Koordinate wird auch mit c multipliziert. Dei Steigung der Tangente wird auch mit c multipliziert.
Begründung solltest du selber mal nachdenken warum das so ist.
Skizze: