2x2 Matrix Eigenwert, Eigenvektoren, Transformations- und Diagonalmatrix.

Question

Jo,

ich habe die folgende Matrix:

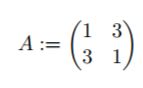
Die Eigenwerte lauten: λ₁=4 und λ₂=-2;

Die Eigenvektoren sind für λ₁=4: span(1 1) und für λ₂=-2: span(1 -1)

Die Aufgabe lautet:

Untersuchen Sie ob die Matrix A diagonalisierbar ist. Bestimmen Sie im Falle der Diagonalisierbarkeit die entsprechenden Transformationsmatrizen.

Also ja die ist diagonalisierbar, da die algebraische Vielfachheit für beide λs (Lambdas) = 1 ist und somit die Geometrische auch.

Die Formel für die Diagonalmatrix lautet: T^-1*A*T=D

Ok und T bildet man doch ganz leicht indem man die Eigenvektoren als Spaltvektoren in eine Matrix schreibt:

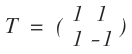
und T^-1 einfach die Obere invertieren:

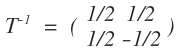
Und alles in die Formel bekommt man für die Diagonalmatrix:

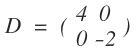
Jetzt kommen wir zu meinem Problem

Ich glaube das ist alles richtig gerechnet ABER nicht die richtige Lösung... unzwar weil ich die λs vertauscht habe und habe somit in die Transformationsmatrix, auch die Eigenvektoren falsch eingesetzt und somit das "verkehrte Ergebnis raus".

Die richtige Lösung sollte das hier sein:

Und das bekommt man ja auch eigentlich wie folgt, indem man einfach die Lambdas in die Diagonale einsetzt:

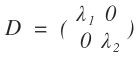
Aber woher weiß ich wie rum ich das einsetzen soll? Ich habe es z.B. falschrum und hab was anderes raus als in der Lösung?

mfg.

Answer 1

Aber woher weiß ich wie rum ich das einsetzen soll? Ich habe es z.B. falschrum und hab was anderes raus als in der Lösung?

Das kannst du dir aussuchen, beide Lösungen sind richtig.Die Eigenwerte kannst du in beliebiger Reihenfolge in der Diagonale anordnen, das ändert dann lediglich die Anordnung der Eigenvektoren. Hauptsache deine T und T^{-1} passen zu deinem D.

Comments

ahso das hab ich mir schon gedacht wollte aber nur sichergehen... mathe eben, man weiß ja nie... vielen dank auf jeden fall