Hi,
b)

c)
m1 = 1.75 √
d)
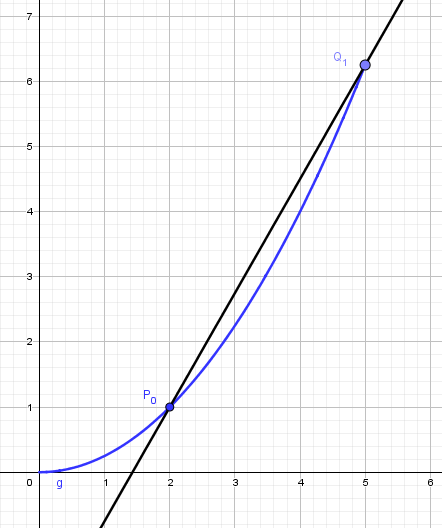
Die Steigung der Flugbahn des Snowboarders beim Verlassen
der Kante der Rampe im Punkt P0 ist geringer als die
Steigung m1. Man bekommt einen genaueren Wert, wenn man den Punkt
Q1 entlang der Parabel näher an den Punkt P0 bringt.
Du hast den Punkt Q2(2.1|1.1025) gewählt und die Steigung der Sekante
durch die Punkte P0 und Q1 ist tatsächlich kleiner als m1, nämlich
m2 = 1.025. √
e)
Die exakte Steigung im Punkt P0 bekommt man durch die Bildung der
ersten Ableitung von f1: f1' = 2*1/4x = x/2 und durch Einsetzen
der x-Koordinate des Punktes P0: f1'(2) = 2/2 = 1.
f)
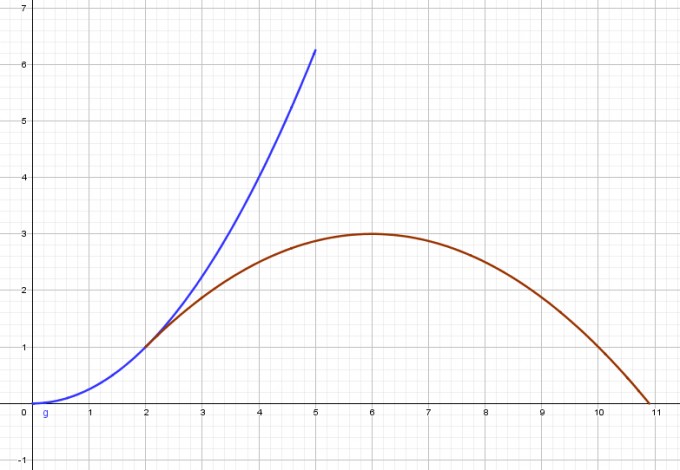
Die Lösung lässt sich aus der Scheitelpunktform ablesen.
An der Stelle x = 6 hat der Snowboarder mit y = 3 die größte Flughöhe. √
g)
-0.125x^2 + 1.5x - 1.5 = 0 lässt sich umformen zu x^2 - 12x + 12 = 0 und die
Anwendung der PQ-Formel liefert zwei Lösungen
x1 = 6 - 2√6 ≈ 1.1 und
x2 = 6 + 2√6 ≈ 10.9
von denen nur x2 ≈ 10.9 brauchbar ist, weil der Snowboarder die Rampe bei x=2 verlässt.
Der Landepunkt ist also L(10.9|0) und für die Sprungweite l = 10.9 - 2 = 8.9
h)
i)
f1(2.1) = 1/4*(2.1)^2 = 1.1025 ≈ 1.1
f2(2.1) = -0.125*(2.1)^2 + 1.5*2.1 - 1.5 = 1,09875 ≈ 1.1
j)
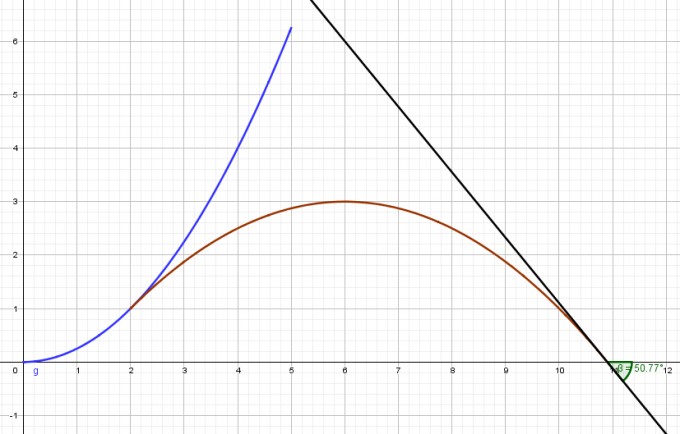
f'(x) = -0.25x + 1.5
f'(6 + 2√6) = -0.25*(6 + 2√6) + 1.5 ≈ -1,22
arctan(-1,22) ≈ -51°
Beste Grüße
gorgar