Vom Duplikat:
Titel: Wahrscheinlichkeitsrechnung, zufällig ergebenden Winkel?
Stichworte: wahrscheinlichkeitsrechnung,stochastik
ich habe eine komplizierte Frage zur Wahrscheinlichkeitsrechnung. Ich versuche mir gerade ein Charakterentwicklungs-System für ein Rollenspiel auszudenken, und da würde ich gerne die Anzahl der Möglichkeiten bzw. deren Wahrscheinlichkeit ausloten.
und zwar habe ich einen Kreis mit einen Mittelpunkt M gegeben. ich habe eine beispielhafte Skizze: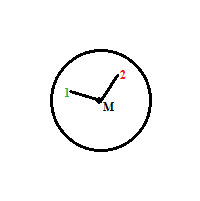
In dem Kreis werden 2 Punkte (1 und 2) zufällig eingezeichnet. Nun werden diese mit 2 Strecken verbunden.
Strecke 1 - M und dann Strecke M - 2. Es ergibt sich, wo die Strecken aufeinandertreffen, nun ein Winkel α bei Punkt M.
Die Fragen, die ich nun habe ist, wie wahrscheinlich ist dieser Winkel 90° ?
Angenommen es werden nach oben genannten Schema 10 Punkte zufällig eingezeichnet, und wie oben miteinander Verbunden. wie wahrscheinlich ist keiner der Winkel: 90°? Wobei es immer nur um die Winkel, die durch die Strecken Punkt X - M ; Punkt M - Y entstehen ginge!
Vielen Dank für jede Antwort im voraus.