Lösen einer Ungleichung: 3/(2x-1)≥ - 5/(x+3)

Question

ich kriege es nicht hin, diese Ungleichung zu lösen.

3/(2x-1) >= - 5/(x+3)

Meine Idee war es erstmal  beide Seiten mit *(2x-1)*(x+3) zu multiplizieren und dann eine Fallunterscheidung zu machen. Aber immer wenn ich das mache, kriege ich die falschen Lösungen raus oder die Bedingungen der Fälle werden nicht erfüllt.

Answer 1

3/(2x-1) >= - 5/(x+3)

Wenn du mit  (2x-1)*(x+3)  multiplizieren willst, musst du ja wissen, ob dieser

Term positiv oder negativ ist; denn mal dreht sich das  >=  Zeichen um

und mal nicht. Also musst du vorher die Fallunterscheidung machen

etwa so:   1. Fall:    (2x-1)*(x+3) > 0   bzw. ( -3 < x < 0,5 )dann wird es

                       3*(x+3)  >= - 5*(2x-1)

und dann  2. Fall:    (2x-1)*(x+3) < 0   bzw. ( x<-3 oder x>0,5 ) dann wird es

                       3*(x+3)  <= - 5*(2x-1) 

Comments

Danke erstmal für die Antwort. So weit bin ich auch bereits gekommen und kriege für den Fall 1 x>= -4/13 und für den zweiten x<= -4/13. Ich weiß aber nicht, wie man nun auf die Lösung kommt. Beim ersten Fall wird -3<x<0,5 erfüllt aber was heißt das dann für die Lösungsmenge?

---

Danke für die Antwort. Ich habe es so berechnet und habe bei beiden fällen die Ungleichung umgeformt, weiß aber nicht wie es nun weiter gehen soll.

---

Zeichne die Zahlen x=-3, x=-4/13 (oder was das ist? eine 13vielleicht?) und x=1/2 auf dem Zahlenstrahl ein. Sie sind von links nach rechts her angeordnet.

Aus dem ersten Fall weisst du, dass x≥ -4/13 ist. Das ist (in diesem Fall) genau für die Zahlen x>1/2 erfüllt. Daher L_(1) = { x Element R | x > 1/2 }

Aus dem zweiten Fall weisst du, dass x≤ -4/13 ist. Das ist (in diesem Fall) genau für die Zahlen -3 < x ≤ -4/13 erfüllt. Daher L_(2) = { x Element R | -3 < x ≤ -4/13 } 

Zusammen: L = L_(1) u L_(2) =  { x Element R | -3 < x ≤ -4/13  oder x>1/2 }

Zahlenwerte ohne Gewähr! Ich kann die Schrift von manfred999 nicht lesen. 

---

Vielen Dank habs endlich verstanden.

Answer 2

Es gilt zunächst herauszufinden wann die
Nenner positiv / negativ sind.
Für x > 1/2 ist der linke Nenner positiv
Für x > - 3 ist der rechte Nenner positiv.
Die beiden Werte habe ich auf einem
Zahlenstrahl markiert.
Es ergeben sich 3 Breiche die getrennt zu
untersuchen sind.

Für den Fall x > 1 / 2 sind beide Nenner
positiv. Bei einer Multiplikation über Kreuz
bleibt das Relationszeichen erhalten.

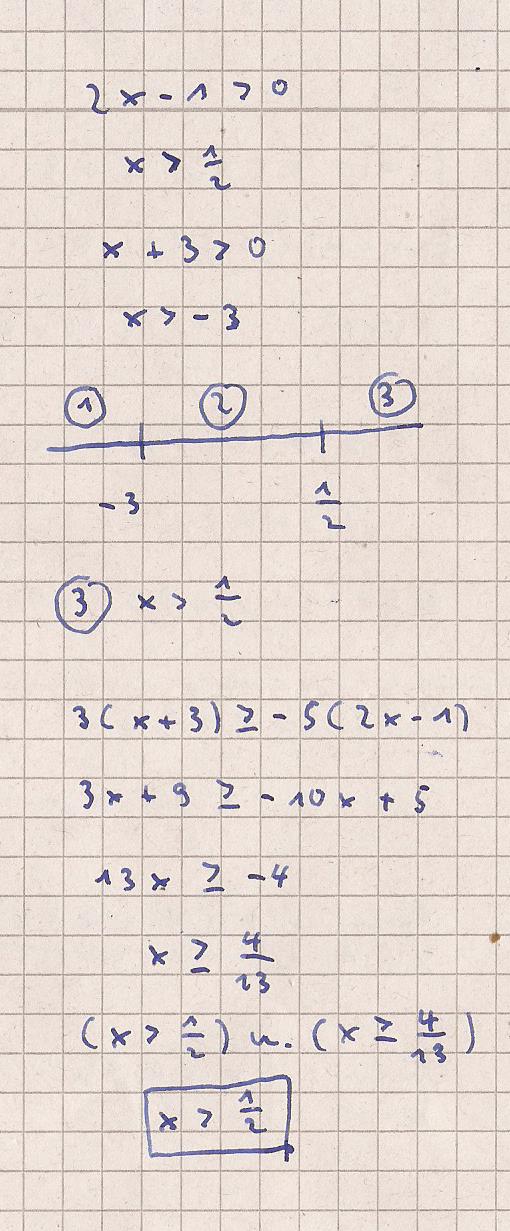
Für denn Fall x < -3 sind beide Nenner negativ.
Bei der Multiplikation über Kreuz bleibt das
Relationszeicen erhalten, da 2 mal mit
etwas negativem multipliziert wird ( = positiv )

Für den Fall 2 wird einmal mit etwas negativem und einmal
mit etwas positivem multipliziert. Das Relationszeichen
muß umgedreht werden.

Im Fall 2 ergibt sich mit der Eingangsvoraussetzung
- 3 < x - 4/13

Die insgesamte Lösungsmenge ist
( x > 1/ 2 ) und  ( - 3 < x - 4/13 )
Die Lösung wurde grafisch überprüft.

Bei Bedarf nachfragen.

Du sollst nicht unwissend sterben.

Comments

Die insgesamte Lösungsmenge ist sicher nicht
( x > 1/ 2 ) und  ( - 3 < x - 4/13 )

Answer 3

3/(2x-1) >= - 5/(x+3)

(13x+4)/((2x-1)*(x+3)) >= 0

(x+4/13)/((x-1/2)*(x+3)) >= 0

Die Vorzeichenwechsel finden also statt bei

-3 oder -4/13 oder 1/2

Die Anzahl der negativen Binome in der letzten Ungleichung muss gerade sein oder es muss x=4/13 gelten. Dies ist äquivalent zu

-3 < x ≤ -4/13 oder 1/2 < x.