Hallo Sweetiii! :-)
Bei einer Multiplikation wäre Dein Rechenweg in Ordnung. Die Zahlen sollen addiert werden, also solltest Du √2·e^{-i π/4} umwandeln: √2·e^{-i π/4} = 1 - i. Dann ist die Addition einfach: (4 - 2i) + √2·e^{-i π/4} = (4 - 2i) + (1 - i) = 5 - 3i.
Was mir noch aufgefallen ist:
√2·e^{-i π/4} hast Du fast richtig umgewandelt. In der Wurzel muss ein + stehen und die -2 muss geklammert sein, denn -2^2 ist nicht gleich (-2)^2 weil -2^2 = -4 und (-2)^2 = 4 ist (*). Schreibe also |z| = √(4^2 + (-2)^2). Setze also eine negative Zahl in Klammern, wenn Du sie potenzieren willst. Bei der Berechnung des Winkels hast Du das Minuszeichen nicht berücksichtigt, es muss φ = arctan(-1/2) heißen.
z = √2·e^{-i π/4}
|z| = √(4^2 + (-2)^2) = √(20)
z = √(20)·(cos(arctan(-1/2)) + i·sin(arctan(-1/2)))
(*)
-2^2 = (-1)·2^2 = (-1)·2·2 = (-1)·4 = -4
(-2)^2 = (-2)·(-2) = 4
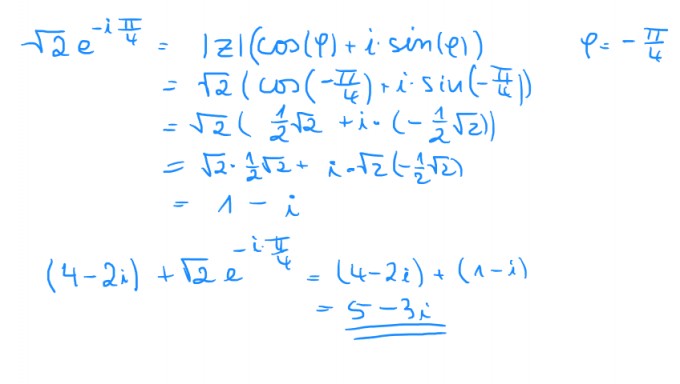
Beste Grüße
gorgar