Bestimmung der Matrix und korrekte Lösung

Question

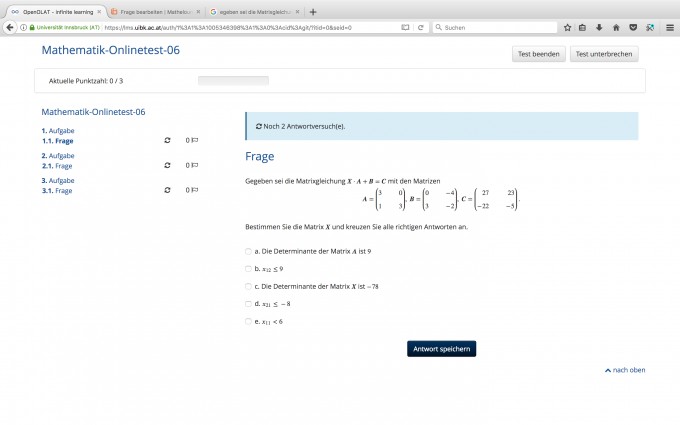
Gegeben sei die Matrixgleichung X·A+B=C mit den Matrizen
Gegeben sei die Matrixgleichung X·A+B=C mit den Matrizen

A=( 3    0 1    3 ), B=( 0    -4 3    -2 ), C=( 27    23 -22    -5 ).

a. Die Determinante der Matrix A ist 9

b. x12 ≤9
c. Die Determinante der Matrix X ist -78
d. x21 ≤-8
e. x11 <6

Es handelt sich jeweils um 2 Kreuz 2 Matrix, die Darstellung ist etwas schwer.
Habe aber auch einen Screenshot der Aufgabe als Bild beigefügt.

Ich habe bei dieser Aufgabe Probleme mit dem erreichen der korrekten Lösung. Habe es nun mehrmals probiert, allerdings scheine ich irgendwo einen Rechenfehler zu haben, weshalb ich nicht auf die korrekte Lösung zu kommen scheine. Falls mir jemand seine Hilfe anbieten könnte, wäre ich sehr dankbar. Sehr gerne auch mit Rechenweg, dann würde es mir leichter Fallen den Fehler ausfindig zu machen.

Vielen lieben Dank.

Comments

vielen Dank für deine schnelle Antwort. Das Problem lag daran, dass ich leichtsinniger Weise die Matrizen fälschlich miteinander verrechnet habe, weshalb ich auf ein vollkommen falsches Ergebnis gestoßen bin.

Deiner Rechnung zufolge müsste dann ja die Lösungsmöglichkeiten a(?) und e(?) korrrekt sein? Vielen lieben Dank für deine immer wieder aufs neue zuverlässigen Beiträge und Lösungen, die du lieferst.

Liebe Grüße

Answer 1

Wo ist das genaue Problem beim Berechnen?

([27, 23; -22, -5] - [0, -4; 3, -2])·[3, 0; 1, 3]^{-1} = [6, 9; -8, -1]

det([6, 9; -8, -1]) = 66