Beweis dafür, dass Integral bei Verschiebung eines Streifens gleichbleibt

Question

Die Aufgabenstellung ist sehr kompliziert, ich poste sie deshalb mal wörtlich, weil ich es kaum verständlich erklären könnte.

Dazu dann dieses Bild.

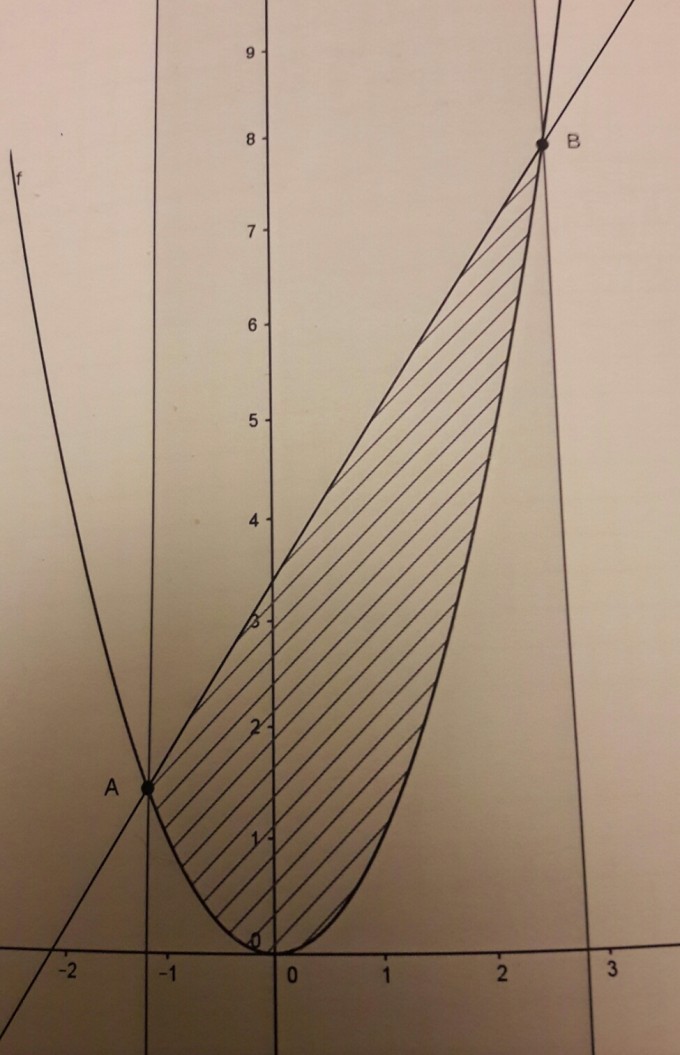
Meine einzige Idee nach wirklich langem Überlegen ist, dass sich beim Verschieben halt die Schnittpunkte ändern und aufgrund der Symmetrie der Normalparabel sich die Flächenabschnitte, die dadurch rausfallen bzw. hinein fallen sich quasi aufheben. Kann aber auch Blödsinn  sein.

Wie weise ich das jetzt nach?

Answer 1

Die Parabel hat die Funktionsgleichung

        f(x) = x².

Die Gerade durch die Punkte A(x_a | f(x_a)) und B(x_b | f(x_b)) hat die Funktionsgleichung

        g(x) = (f(x_b)-f(x_a))/(x_b-x_a) · (x-x_a) + f(x_a).

Dabei ist x_b = x_a + 4.

Bestimme ∫_xa..xb (g(x) - f(x)) dx.

Comments

Danke auf jeden Fall erstmal, geht mir aber fürs Verständnis etwas zu schnell. Wie kommt man auf diese Funktionsgleichung der Geraden?

---

Das ist die Zweipunkteform für Geraden. Eine Gerade durch die Punkte (x₁ | y₁) und (x₂ | y₂) hat die Gleichung y = (y₂ - y₁)/(x₂ - x₁) · (x - x₁) + y₁.

Wer die Zweipunkteform nicht auswendig lernen will, der kann auch die Punkte in die allgemeinen Geradengleichung y = mx + n einsetzen und das lineare Gleichungssystem lösen.

Oder man argumentiert damit, dass die Gerade wegen Steigungsdreieck die Steigung m = (y2 - y1)/(x2 - x1) hat, aber gegenüber der Funktion y = mx um x₁ horizontal und um y₁ vertikal verschoben wurde.

---

Kann man das auch ohne diese Zweipunkteform begründen? Verstehe den Hintergrund zwar, aber glaube nicht, dass das so gedacht ist, habe von dieser Form noch nie gehört vorher.

---

Ja, mit linearen Gleichungssystemen. Das Verfahren müsste in Klasse 7 oder 8 duchgesprochen worden sein, darfst du also sicherlich verwenden.

Verschieben von Funktionen wird normalerweise auch lange vor Integralrechnung bespochen, sollte also ebenfalls vewendet werden dürfen.

---

Du hast deine Antwort doch nochmal geändert oder? Hatte von dem mit dem Gleichungssystem vorher nichts gelesen.

Habe jetzt auch irgendwie Probleme beim Aufstellen des Gleichungssystems, aufgrund der vielen Variablen.

Sind die Gleichungen so richtig?

f (xa) = m*xa+b

f (xa+4)= m*xa+4+b

---

> f (xa+4)= m*xa+4+b

Da kommt eine Klammer um das xa+4, sonst wird nur das xa mit der Steigung multipliziert und die 4 wird Teil des y-Achsenabschnitts:

        f (xa+4)= m*(xa+4)+b

---

Wow ich glaube ich habe es jetzt hinbekommen.

Bekomme dann die allgemeine Gleichung y= 2(xa+2)*x-xa(xa+4) raus. Wenn ich da für xa etwas einsetze bekomme ich die gleiche Geradengleichung raus, wie als ich das Gleichungssystem mit Zahlen gelöst habe. Sollte also stimmen. Wirklich danke.