a)
Ansatz
v(t) = at^3 + bt^2 + ct + d
v'(t) = 3at^2 + 2bt + c
Gesucht sind die Koeffizienten a, b, c und d.
Aus dem Text lesen wir die Bedingungen heraus:
Lokales Geschwindigkeitsminimum 0,5m/s bei t0 = 0 und bekommen daraus
die beiden Gleichungen
1)
v(0) = 0,5
a·(0)^3 + b·(0)^2 + c·(0) + d = 0,5
d = 0,5
2)
v'(0) = 0
3a·(0)^2 + 2b·0 + c = 0
c = 0
Die weiteren Bedingungen sind:
Maximale Geschwindigkeit 0,8m/s bei t=3
Aus diesen Informationen bekommen wir zwei weitere Gleichungen
3)
v(3) = 0,8
a·(3)^3 + b·(3)^2 + c·3 + d = 0,8
27a + 9b + 0,5 = 0,8 |-0,5
27a + 9b = 0,3
4)
v'(3) = 0
3a·(3)^2 + 2b·3 + c = 0
27a + 6b = 0
Die Koeffizienten c und d mit c = 0 und d = 0,5 haben wir schon berechnet.
Es fehlen noch die Koeffizienten a und b.
Für die Berechnung von a und b nehmen wir die Gleichungen unter 3) und 4)
die das lineare Gleichungssystem bilden:
27a + 9b = 0,3
27a + 6b = 0
Wir ziehen die zweite Gleichung von der ersten ab und erhalten
3b = 0,3 |:3
b = 0,1
b = 0,1 setzen wir in die zweite Gleichung ein
27a + 6·0,1 = 0
27a + 0,6 = 0 | -0,6
27a = -0,6 |:27
a = -0,022
Wir haben alle Koeffizienten berechnet, die wir in die Funktionsgleichung v(t) = at^3 + bt^2 + ct + d einsetzen.
v(t) = -0,022·t^3 + 0,1·t^2 + 0,5
Der gesuchte Term steht rechts vom Gleichheitszeichen.
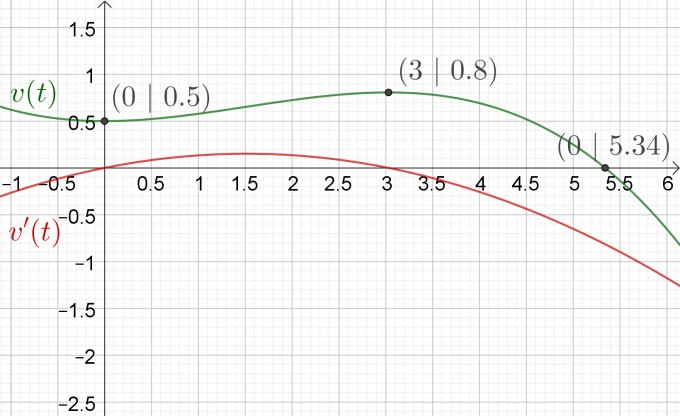
b)
Wir setzen -0,022·t^3 + 0,1·t^2 + 0,5 = 0 und berechne die Nullstelle t = 5,34
c)
Die Beschleunigung ist die Ableitung der Geschwindigkeit nach der Zeit,
das ist in unserem Fall v'(t) = 3at^2 + 2bt + c.
Der Zeitpunkt des Stillstandes ist t = 5,34 den wir bloß
noch zusammen mit den Koeffizienten
a = -0,022
b = 0,1
c = 0
in die Ableitung v'(t) einzusetzen brauchen.
v'(t) = 3at^2 + 2bt + c.
v'(t) = 3*(-0,022)*( 5,34 )^2 + 2*0,1*5,34
v'(t) -0,81
Die Verzögerung zum Zeitpunkt t = 5,34 beträgt a = -0,81 m/s^2
d)
v'(0) = 0
Grüße