Wie lautet der Funktionsterm 3 Grades?

Question

Der Graph einer ganzrationalen Funktion dritten Grades berührt die x-Achse an der Stelle 4 und hat an der stelle 8/3 ( Wurde als bruch geschrieben) eine wendestelle. Die Wendetangente hat die Steigung -4/3 ( auch als bruch geschrieben worde und das " - " befindet sich vor dem bruch und nicht direkt vor dem nenner oder zähler ).

Ich bräuchte nur die 4 punkte mit denen ich dann dann bis zum gleichungssystem komme ! Ab dort würde ich keine hilfe mehr brauchen.

Answer 1

f(4) = 0
f'(4) = 0
f"(8/3) = 0
f'(8/3) = -4/3

64·a + 16·b + 4·c + d = 0
48·a + 8·b + c = 0
16·a + 2·b = 0
64/3·a + 16/3·b + c = -4/3

f(x) = 0,25·x³ - 2·x² + 4·x
f'(x) = 0,75·x² - 4·x + 4
f''(x) = 1,5·x - 4
f'''(x) = 1,5

Plotlux öffnen

f₁(x) = 0,25·x³-2·x²+4·xf₂(x) = -4/3·(x-8/3)+32/27

Answer 2

f(4)=0

f'(4)=0

f"(8/3)=0

f'(8/3)=-4/3

Comments

Was bedeutet "Paypal-Spende als Dankeschön für die Hilfe von koffi123 senden."?
Flaschensammeln in digital?

---

Danke für die schnelle Antwort .

Ich hätte noch eine Frage bezüglich der Brüche ! Es ist ja geschrieben , dass an der Stelle 8/3 ( Als bruch ) eine Wendestelle ist . Also gibt der Bruch den x-wert an und nicht auch y ? Sprich 3 nach rechts und 8 nach oben wäre falsch . Und mit 8/3 ist dann gemeint 2.666666.. als x wert ?

Mich verwirren leider immer die kleinen Sachen !

---

Sozusagen, du kannst dich via PayPal bei mir bedanken wenn du möchtest.

---

Möchte ich nicht, ich mag PayPal nicht...

---

Genau, mit 8/3 ist 2,666666 gemeint. Da man bei dieser Darstellung aber Genauigkeit verliert (Rundung) wird stattdessen der exakte Bruch verwendet.

---

Ok, auch gut.

---

@az0815:

siehe hier 

https://www.mathelounge.de/514458/individuelles-bedanken-mitgliedern…

---

Interessant. Gib mal Bescheid, wenn sich hier irgendjemand bei dir bedankt. Viele drücken ja nicht mal auf den Daumen nach oben, wenn ihnen die Antwort geholfen hat.

---

Ja das stimmt. Ich habe gesehen dass man jetzt die Möglichkeit hat den Link einzutragen und wollte mal sehen ob das jemand nutzt. Grundsätzlich finde ich die Idee nicht schlecht. Aber es sind ja hier auch viele Schüler unterwegs, die vermutlich gar kein PayPal Konto haben. Insofern weiß ich nicht ob das erfolgreich sein wird. Bisher hat sich niemand auf diesem Weg bedankt. Aber ich sag Bescheid wenn es jemand mal tun sollte.

Answer 3

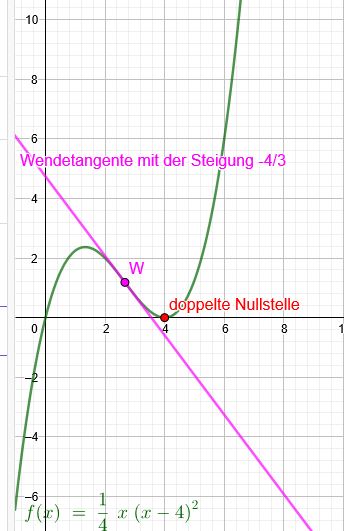
berührt die x-Achse an der Stelle $x=4$

→ bedeutet doppelte Nullstelle:

$f(x)=a[(x-4)^2(x-N)]$

$f'(x)=a[(2x-8)(x-N)+(x-4)^2]$

$f''(x)=a[(2x-2N)+(2x-8)+(2x-8)]\\=a[(2x-2N)+4x-16]$

hat an der Stelle $x=\frac{8}{3}$  eine Wendestelle:

$f''(\frac{8}{3})=a[(2 \cdot \frac{8}{3}-2N)+4\cdot \frac{8}{3}-16]=0$

 $N=0$:

$f'(x)=a[(2x-8)\cdot x+(x-4)^2]$

Die Wendetangente hat die Steigung $-\frac{4}{3}$:

$f'(\frac{8}{3})=a[(2\cdot \frac{8}{3} -8)\cdot \frac{8}{3}+(\frac{8}{3}-4)^2]=-\frac{4}{3}$

$a=\frac{1}{4}$:

$f(x)=\frac{1}{4}[x(x-4)^2]$